|
50.5 emprunt bancaire premiers calculs JS |
 See You Why? |
Avant de démarrer dans la programmation en JavaScript de ces calculs relatifs aux emprunts, nous conseillons au lecteur de prendre connaissance des formules expliquées ici.
Rappelons l'essentiel ici :
en supposant V, le montant emprunté et reçu au début de l'emprunt,
r (=rate), le taux d'intérêt (annuel ou mensuel) de l'emprunt,
a, l'annuité ou mensualité à rembourser (selon le choix pour r et n),
n, le nombre d'années ou mensualités du remboursement :
V = a . [1-1/(1+r)n] = 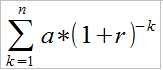
. r
a = V . r
1-1/(1+r)n
Dans notre chapitre 27 du cours de comptabilité et gestion, nous avons déjà signalé que "Dans le cas d'annuités constantes qui permettent de rembourser en totalité l'emprunt en n périodes, les amortissements forment une suite géométrique de raison (1+r) et la formule de l'annuité ou mensualité a peut être exprimée en fonction des autres données V, r et n." Notre propos n'est pas de réaliser un cours de math, mais le lecteur intéressé recherchera dans un moteur de recherche les mots clés et soulignés de cet énoncé. Plusieurs résultats intéressants, dont http://www2.cndp.fr/archivage/valid/81023/81023-12675-16022.pdf dont un exemplaire ici.
Cette fonction est appliquée dans chaque input de type 'text'. Son but est de vérifier le nombre de décimales de toutes valeurs qu'on y écrit, que ce soit l'utilisateur qui entre une valeur ou le programme JS qui en calcule puis écrit une.
Concrètement, il s'agit de remplacer une virgule décimale par un point décimal ;
et de supprimer tout caractère non alphanumérique au début ou à la fin de la donnée.
On utilisera la fonction replace() vue lors des manipulations sur les chaines de caractères (voir ici) ainsi que les expressions régulières vues dans la séquence suivante (voir ici).
En voici la source :
function maj_valeur (input) {
var temp;
input.value=input.value.replace(',','.');
input.value=(input.value.replace(/^\W+/,'')).replace(/\W+$/,'');
if (input.value != null && input.value.length != 0) {
temp = "" + eval(input.value);
} else {
input.value = "0.00";
}
}
Son nom l'indique, il s'agira de calculer le montant emprunté (V) à condition de connaitre les trois autres éléments qu'il faudra aller lire là où ils se trouvent dans le formulaire :
Nos lecteurs sont remplis de bon sens.
Si r est un taux d'intérêt annuel,
le nombre de paiements sera la durée du crédit en années
et le remboursement se fera annuellement (pas mensuellement) ;
si r est un taux d'intérêt mensuel (annuel divisé par 12),
le nombre de paiements sera la durée du crédit en mois
et le remboursement se fera mensuellement.
Le lecteur se rappellera que :
a * [1-1/(1+r)n ] = V
r
On se rappellera aussi que JS n'est pas très typé... cependant les valeurs lues dans un formulaire sont souvent considérées comme des valeurs de type string et des calculs ne peuvent se faire que sur des variables numériques. Plusieurs techniques sont applicables pour transformer des variables string en variables numériques.
Plutôt que de préciser les avantages et inconvénients, les précautions à prendre, nous préférons illustrer chacune des fonctions avec votre plate-forme, votre navigateur et votre ordinateur pour comparer chaque formule... et si vous n'y trouvez pas votre compte, à vous d'essayer...
| chaine | parseFloat(chaine); | parseInt(chaine); | eval(chaine); | 1.0*chaine; |
|---|---|---|---|---|
| "135.68" | 135.68 | 135 | 135.68 | 135.68 |
| "135,68" | 135 | 135 | 68 | NaN |
| "12.3E-6" | 0.0000123 | 12 | 0.0000123 | 0.0000123 |
| "SeeYouWhy" | NaN | NaN | NaN | |
| "24.568SeeYouWhy38" | 24.568 | 24 | NaN | |
| "SeeYouWhy38.24" | NaN | NaN | NaN | |
| "AF8BEF" | NaN | NaN | NaN | |
| "0284" | 284 | 284 | 284 | 284 |
| "0xAB882F" | 0 | 11241519 | 11241519 | 11241519 |
| "12.1*6" | 12.1 | 12 | 72.6 | NaN |
| "cos(3.1)" | NaN | NaN | NaN | |
| "Math.cos(3.1-2)" | NaN | NaN | 0.4535961214255773 | NaN |
| "2.1^3" | 2.1 | 2 | 1 | NaN |
Si l'on n'oublie pas que l'objet form qui est passé comme argument de la fonction possède des proprités, la lecture des données du formulaire et le calcul du montant emprunté pourrait se faire ainsi :
calcul_montantemprunte(form) {
var Vx, R, N, Y, A;
if((form.rate.value.length == 0) || (form.num.value.length == 0) ||
(form.num_annum.value.length == 0) || (form.amount.value.length == 0)) {
form.loan.value = "0.00";
} else {
R = eval(form.rate.value) / 100.0;
// transforme 4% en 0.04
N = eval(form.num.value);
Y = eval(form.num_annum.value);
//Y est pour l'instant inadéquat, il devrait enregister le nbre de paiements par an
// par défaut, on lui attribue la valeur de 12
A = eval(form.amount.value);
if(Y == 0.0) {
Vx = 0.0;
} else {
//formule pour le calcul via la formule avec Σ
//Vx = A * (1.0 - binomial(R / Y, -N)) / (R / Y);
Vx = A / R * (1.0 - 1 / (Math.pow((1+R),N)));
Vx = Vx * 100;
Vx = Math.round(Vx);
Vx = Vx / 100;
}
form.loan.value = "" + Vx;
}
}
Cette routine aurait aussi pu vérifier les ordres de grandeur des données :
* R supérieur à 0, mais inférieur à 20 (rappelons-nous les années 80);
* N supérieur à 1, mais inférieur à ??? selon qu'il soit exprimé en mois ou en année.
Ici aussi son nom l'indique, il s'agira de calculer le montant payé périodiquement (a) (appelée annuité ou mensualité) à condition de connaitre les trois autres éléments qu'il faudra aller lire là où ils se trouvent dans le formulaire :
Depuis la lecture du paragraphe précédent, nos lecteurs sont toujours aussi remplis de bon sens.
Si r est un taux d'intérêt annuel,
le nombre de paiements devra être la durée du crédit en années
et le remboursement se fera annuellement (pas mensuellement) ;
si r est un taux d'intérêt mensuel (annuel divisé par 12),
le nombre de paiements sera alors la durée du crédit en mois
et le remboursement se fera mensuellement.
Le lecteur se rappellera que :
a = V . r
1-1/(1+r)n
La source de cette routine, présentée ici devrait supporter les mêmes remarques que celle développée pour le calcul du montant imposé :
function calcul_mensualite(form) {
var V, R, N, Y, Ax;
if((form.loan.value.length == 0) || (form.rate.value.length == 0) || (form.num.value.length == 0) || (form.num_annum.value.length == 0)) {
form.amount.value = "0.00";
} else {
V = eval(form.loan.value);
R = eval(form.rate.value) / 100.0;
// transforme 4% en 0.04
N = eval(form.num.value);
Y = eval(form.num_annum.value);
//Y est pour l'instant inadéquat, il devrait enregister le nbre de paiements par an
// par défaut, on lui attribue la valeur de 12
if (Y == 0.0) {
Ax = 0.0;
} else {
//formule pour le calcul via la formule avec Σ
//Ax = V * R / Y / (1.0 - binomial(R / Y, -N));
Ax = V * R / (1.0 - 1 / (Math.pow((1+R),N)));
Ax = Ax * 100;
Ax = Math.round(Ax);
Ax = Ax / 100;
}
form.amount.value = "" + Ax;
}
}
Ici, l'algèbre financière ne donne pas de réponse... impossible d'isoler la variable R dans l'équation de base... Ne soyons pas perdu pour si peu, l'ordinateur calcule vite et nous pouvons faire des essais successifs en veillant à se rapprocher de la vérité.
Imaginez que vous ayez à deviner un nombre compris entre 1 et 20000 et que votre interlocuteur à chaque essai vous réponde "trop petit" ou "trop grand". Si à chaque essai vous choisissiez la valeur moyenne entre les extrémités de l'espace qui vous reste, vous y arriverez vite.
Un essai, je choisis 4689, à vous de jouer :
je dis 10000 (milieu de 1 à 20000), vous répondez "-" ;
je dis 5000 (milieu de 1 à 10000), vous répondez "-" ;
je dis 2500 (milieu de 1 à 5000), vous répondez "+" ;
je dis 3750 (milieu de 2500 et 5000), vous répondez "+" ;
je dis 4375 (milieu de 3750 à 5000), vous répondez "+" ;
je dis 4687 (milieu de 4375 à 5000), vous répondez "+" ;
je dis 4844 (milieu de 4687 à 5000), vous répondez "-" ;
je dis 4766 (milieu de 4687 à 4844), vous répondez "-" ;
je dis 4726 (milieu de 4687 à 4766), vous répondez "-" ;
je dis 4707 (milieu de 4687 à 4726), vous répondez "-" ;
je dis 4697 (milieu de 4687 à 4707), vous répondez "-" ;
je dis 4692 (milieu de 4687 à 4697), vous répondez "-" ;
je dis 4689 (milieu de 4687 à 4692), vous répondez "Gagné !"
Merci pour le jeu, mais cela n'explique pas comment trouver le taux auquel je dois emprunter (V) pendant (n) années en remboursant (A) par an... la question n'est peut-être pas celle que l'on se pose d'habitude, mais essayons de trouver ce taux mystérieux, normalement situé entre les extrêmes de 0,1% à 2000%, soit de 0,001 à 20...
Chaque fois, je calcule le taux moyen des deux extrêmes,
je calcule l'annuité à payer à ce nouveau taux imaginaire (pour un emprunt V connu pour une durée n connue) puis
je compare l'annuité A connue et l'annuité calculée,
si l'annuité calculée est plus grande que l'annuité connue, je dois baisser mon taux sinon... je dois le relever.
Essayons cela :
function calcul_taux(form) {
var V, Rx, N, Y, A;
if((form.loan.value.length == 0) || (form.num.value.length == 0) || (form.num_annum.value.length == 0) ||
(form.amount.value.length == 0)) { form.rate.value = "0.00";
} else {
V = eval(form.loan.value);
N = eval(form.num.value);
Y = eval(form.num_annum.value);
A = eval(form.amount.value);
if (Y == 0) {
I = 0.0;
} else {
var taux_bas, taux_haut, taux_moyen, err_taux_moyen;
var i_compteur;
taux_bas = 0.001;
taux_haut = 10.0;
i_compteur = 0;
while(i_compteur < 30) {
i_compteur = i_compteur + 1;
taux_moyen = (taux_haut + taux_bas) / 2.0;
err_taux_moyen = erreur(V, taux_moyen, N, Y, A);
if (err_taux_moyen == 0.0) {
break;
}
if(err_taux_moyen < 0.0) {
taux_bas = taux_moyen;
continue;
}
if(0.0 < err_taux_moyen) {
taux_haut = taux_moyen;
continue;
}
}
taux_moyen = taux_moyen * 1000;
taux_moyen = Math.round(taux_moyen);
taux_moyen = taux_moyen / 1000;
Rx = taux_moyen * 100.0;
}
form.rate.value = "" + Rx;
}
}
Reste à définir comment calculer cette erreur.
Comme annoncé, je calcule l'annuité à payer à ce nouveau taux imaginaire (pour un emprunt V connu pour une durée n connue) puis
je compare l'annuité A connue et l'annuité calculée,
si l'annuité calculée est plus grande que l'annuité connue, je dois baisser mon taux sinon... je dois le relever.
function erreur(Empruntconnu, Imoyen, Nconnu, Y, Aconnu) {
var difference, ann_calculee;
ann_calculee = Empruntconnu * Imoyen / (1.0 - 1 / (Math.pow((1+Imoyen),Nconnu)));
difference = Aconnu - ann_calculee;
return difference;
}
Et voilà terminé notre calculateur d'emprunt... et bien non !
Reste le cas pas fréquent de ceux qui veulent emprunter qui n'ont pas de pression possible pour modifier le taux, mais qui peuvent faire varier la durée de l'emprunt.
Qu'ils n'oublient cependant pas que pendant la première moitié de la durée de l'emprunt, on ne rembourse presque pas de capital, on ne paie quasi que des intérêts... ce n'est que pendant le dernier tiers du temps que le capital est remboursé... les curieux qui veulent s'en rendre compte pourront le vérifier sur tableur en lisant ceci.
Comme annoncé, ceux qui souhaiteraient raccourcir ou allonger la durée de l'emprunt, donc le nombre d'annuités et/ou de mensualités auront droit à tester leur possibilité de remboursement en utilisant le bouton prévu en troisième position de notre calculateur. Pas de formule à notre disposition dans un traditionnel cours d'algèbre financière... peu importe.
Nous venons de découvrir la technique des essais successiffs, nous pourrons l'appliquer ici aussi :
cela n'explique pas comment trouver la durée pendant laquelle je dois emprunter (V) à un taux (R) en remboursant (A) par an... la question n'est peut-être pas celle que l'on se pose d'habitude, mais essayons de trouver cette durée mystérieuse, normalement située en deça de 100 ans ou 1200 mois... et comme nous savons que nous devrons chaque fois diviser l'espace en deux, prenons la valeur maximale la plus proche et qui soit une puissance de 2... 1024 semble correct (les emprunts aussi longs sont à déconseiller...)
Ici aussi, je calculerai l'annuité à payer pour cette nouvelle durée imaginaire (pour un emprunt V connu pour un taux R connu) puis
je compare l'annuité A connue et l'annuité calculée,
si l'annuité calculée est plus grande que l'annuité connue, je dois diminuer la durée sinon... je dois l'augmenter.
Ceci est tellement proche de la démarche faite pour la recherche du taux que je pourrais peut-être employer la même fonction. À nous d'essayer :
function calcul_nbre_mensualite(form) {
var P, I, N, Y, M;
var V, R, Nx, Y, A;
if((form.loan.value.length == 0) || (form.rate.value.length == 0) || (form.num_annum.value.length == 0) || (form.amount.value.length == 0)) {
form.num.value = "0.00";
} else {
V = eval(form.loan.value);
R = eval(form.rate.value) / 100.0;
Y = eval(form.num_annum.value);
A = eval(form.amount.value);
if (Y == 0) {
Nx = 0.0;
} else {
var duree_bas, duree_long, duree_mid, err_mid;
var i_compteur;
duree_bas = 0;
duree_long = 1024;
i_compteur = 0;
while(i_compteur< 15) {
i_compteur = i_compteur + 1;
duree_mid = (duree_long + duree_bas) / 2.0;
err_duree = erreur(V, R, duree_mid, Y, A);
if(err_duree == 0.0) {
break;
}
if (0.0 < err_duree) {
duree_bas = duree_mid;
continue;
}
if (err_duree< 0.0) {
duree_long = duree_mid;
continue;
}
}
Nx = duree_mid; Nx = Math.round(Nx * 100)/100;
}
form.num.value = "" + Nx;
}
}
Et maintenant, tout est réellement fini... il ne vous reste plus qu'à tester et retester cette page que nous avons créée ensemble.
Bon amusement.
Merci de votre visite à partir de :
| Vous voulez lire quelques messages reçus ? qui ne compte chaque nouvel ordinateur visiteur qu'une seule fois m-à-j du 22/11/2021 : Depuis cette fin septembre 2009, parmi les 210 pays (sur 274 drapeaux connus) qui nous ont visité, voici les 100 pays qui nous visitent le plus, Nos petits visiteurs, classés par date de visite, où un seul ordi nous a visité, sont : 199. Turkmenistan (TM May 10, 2017) ; 200. Lesotho (LS March 1, 2017) ; 201. Turks and Caicos Island (TC January 18, 2016) 202. Cook Islands (CK September 19, 2015) 203. Faroe Islands (FO January 27, 2015) 204. Virgin Islands American (VI November 12, 2014) ; 205. Belize (BZ September 29, 2014) ;206. Eswatini - Swaziland (SZ July 21, 2014) ; 207. Grenada (GD April 3, 2014) ; 208. Timor-Leste (TI March 29, 2014) ; 209. American Samoa (AS December 26, 2012) ; 210. Guyana (GY November 5, 2010). |