|
Algèbre financière par Excel Exercice sur les emprunts et amortissement du capital emprunté |
 |
Vous rêvez d'acheter une maison,
vous décidez donc d'emprunter 150 000 € pendant 30 ans ;
le taux d'intérêt est de 10 %.
Pour vous éviter de faire des calculs longs et difficiles, nous allons employer Excel® de Microsoft®.
I. Données et disposition du tableau
III. La fonction SI(;;)
IV. Adresse absolue ou relative
V. Les formules d'emprunt : adresse absolue ou relative
VI. Le calcul de l'intérêt annuel
VII. La part de capital remboursée
VIII. Solde restant dû en fin d'année
XI. Allongement de la durée d'emprunt
XII. Total de capital et d'intérêt
XIII. Format monétaire
Le fichier Excel solution du problème

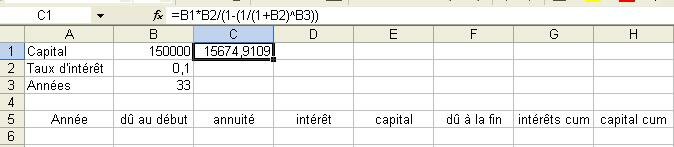
Les premières lignes serviront à introduire les données du problème.
En B1, vous indiquerez le capital emprunté (ici 150 000 €,
attention, pas d'espace dans les nombres pour Excel) ;
en B2, vous indiquerez le taux d'intérêt (ici 10 %,
qui se notera 0,1 ou 10/100) ;
en B3, vous indiquerez le nombre d'années (ici 30 ans prévus,
même si on lit 33) .
Passez immédiatement à la ligne 5,
Dans la première colonne,
vous notez "Année",
vous mettrez ensuite (lignes 6 et suivantes) toutes les années jusque la dernière c'est-à-dire jusque 30 ans (si vous vous étonnez de voir 33, vous comprendrez pourquoi un peu plus tard).
Dans la deuxième colonne,
vous notez "dû au début",
vous mettrez ensuite le montant que vous devez au début de chaque année (pour rappel, le montant dû en début d'année est le même que celui dû en fin d'année précédente... sauf pour la première année).
Dans la troisième colonne,
vous notez "annuité",
vous mettrez ensuite le montant à payer chaque année (qui sera toujours le même puisqu'on travaille en annuités constantes).
Dans la quatrième colonne,
vous notez "intérêt",
vous mettrez dans cette colonne les intérêts à payer, qui seront calculés sur le montant dû en début d'année (voir 2e colonne).
Dans la cinquième colonne,
vous notez "capital",
vous y calculerez le capital remboursé cette année-là (ce sera le montant de l'annuité constante, diminué du montant d'intérêts calculé en 4e colonne.
Dans la sixième colonne,
vous notez "dû à la fin",
vous y calculerez le montant dû à la fin (ce sera le montant du capital dû en début [voir colonne 2] diminué du capital remboursé cette année-là [voir colonne 5].
Dans la septième colonne,
vous notez "intérêts cumulés",
vous y calculerez le total des intérêts payés jusqu'à la fin de l'année en cours (ce sera le montant des intérêts cumulés de l'année précédente [voir ligne supérieure] augmenté des intérêts payés cette année-là [voir colonne 4].
Dans la huitième colonne,
vous notez "capital cumulé",
vous y calculerez le total de capital payé jusqu'à la fin de l'année en cours (ce sera le montant de capital cumulé de l'année précédente [voir ligne supérieure] augmenté capital remboursé cette année-là [voir colonne 5].
Pour ne pas écrire toutes les années jusque l'année 30,
sélectionner dans la cellule année le nombre 1,
et étirer jusque l'année 30 en appuyant sur CTRL (en permanence) pour que ça aille en augmentant (mieux, en s'incrémentant).
Si vous n'appuyez pas sur CTRL, le tableur Excel recopiera le nombre 1 dans toutes les cellules.

Combien faudra-t-il rembourser ?
Employez cette formule :
Excel a prévu une fonction financière intégrée VPM, dont la syntaxe est VPM(taux_par_période, nombre_de_périodes, valeur_actuelle).
Ici,
* taux_par_période serait : B2/12 car 10 % est le taux annuel, mais les remboursements mensuels, donc il faut diviser le TAEG par 12 ;
* nombre_de_périodes serait : B3*12 car les 33 ans correspondent à 31*12 versements mensuels ;
* valeur_actuelle est : B5 c'est-à-dire le capital emprunté aujourd'hui
(si la valeur négative du résultat vous gêne, n'hésitez pas à placer un signe 'moins' devant ce capital emprunté).
Un lecteur un peu plus pointu pourrait même nous reprocher de ne pas tenir compte des intérêts mensuels sur les intérêts, il n'aurait pas tort.
Le nouveau taux_par_période devrait donc être (1+B2)^(1/12)-1 pour être tout-à-fait rigoureux et exact.
Ici, nous avons préféré introduire la formule de calcul étudiée au cours d'algèbre financière.
Annuité =
. Capital emprunté V * Taux d'intérêts r .
1-1/(1+le taux d'intérêt r) exposant le nombre d'années n
et donc ici,
= B1 * B2 / (1-(1/(1 + B2) ^ B3))
Comme pour la formule financière intégrée à Excel, on pourrait pu
* remplacer B2 par B2/12 pour le taux d'intérêt, [ou plus précisémént par (1+B2)^(1/12)-1]
* remplacer B3 par B3*12 pour le nombre de versements
et obtenir alors la mensualité au lieu de l'annuité.
(le lecteur aura remarqué que les parenthèses notées en vert sont inutiles, compte tenu de la priorité des opérations) ;
autre présentation de la formule (voir seconde formule qui permet de trouver l'annuité 'a') :
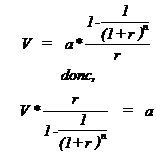 |
Pour ceux qui voudraient savoir d'où vient cette formule, cliquer ici.
Pour rappel :
Aux lecteurs français, qui seraient tentés de repousser cette méthode de calcul sous prétexte qu'elle soit basée sur une année lombarde, nous répondons que le TAEG proposé est un taux annuel effectif global, qui ne tient pas compte des longueurs des mois (l'ancienne habitude des financiers étant de travailler sur une année faite de 12 mois de 30 jours). Selon les pays, le calcul mensuel pourrait ne pas répondre aux dispositions légales en vigueur dans leur pays (rappelons que CUY est un site belge... à chacun de s'y adapter). [Merci pour cette remarque, Patrice] Le code de consommation français ne met donc pas en cause ce calcul annuel.
On constate au fur et à mesure que les années passent que la part des intérêts à rembourser devient de plus en plus faible, alors que la part en capital ne cesse d'augmenter.
Pourquoi ?
Les intérêts sont calculés sur le montant à rembourser.
Les premières années, le montant à rembourser est important donc les intérêts sont très élevés.
Alors que plus les années passent,
plus le montant à rembourser diminue,
donc les intérêts diminuent également ;
et comme les annuités sont constantes,
le capital remboursé chaque année va en augmentant avec le temps.
Pour pouvoir voir la fin du travail en voyant toujours bien les intitulés des colonnes, il faut figer les volets.
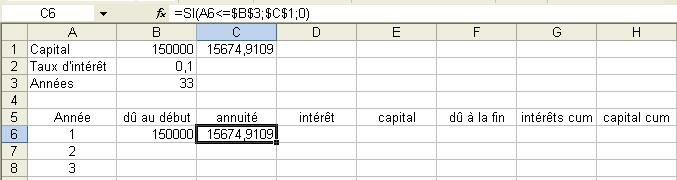
Pour les annuités, on utilise une formule avec " SI ".
La syntaxe de la condition est :
=SI (condition ; valeur si vraie ; valeur si faux)
La condition est une expression logique, comme par exemple ici, en C6, on utilise : A6<=$B$3 ;
la valeur à noter si la condition est vraie est l'annuité, calculée ici en C1 ;
sinon, la valeur est nulle, ou ici 0.
Cette formule veut donc dire :
si l'année qu'il y a dans la cellule A6 est plus petite ou égale au nombre d'années introduit en B3 (ici, à 33 ans),
alors la valeur (si vraie) à mettre est le montant de l'annuité à rembourser (calculée dans la cellule C1),
sinon on indique 0.
Cela veut bien dire que :
si on n'a pas atteint la 30e (ou 33e) année,
alors on devrait rembourser l'annuité,
sinon (si la 30e année est atteint), le montant à rembourser sera de 0 €.
La présence et l'utilité du signe $ dans les formules sera expliquée dans l'étape suivante (adresse absolue avec, adresse relative sans).
La différence entre adresse absolue et relative a été expliquée dans la théorie (voir ici).
Le lecteur se rappellera que si en C6, on utilise : A6<=$B$3, Excel comprendra : LC(-2)<=$B$3
c'est à dire, la cellule située même ligne 6, et deux colonnes à gauche <= la cellule absolue $B$3.
Cette formule recopiée dans d'autres cellules, donnera les résultats suivants : LC(-2)<=$B$3 :
recopiée en D6 donnerait : B6<=$B$3 recopiée en F6 donnerait : D6<=$B$3 recopiée en C7 (*) donnerait : A7<=$B$3 recopiée en D10 donnerait : A10<=$B$3 recopiée en F11 donnerait : D11<=$B$3 et on constate que la formule, recopiée dans la cellule inérieure, est correcte.
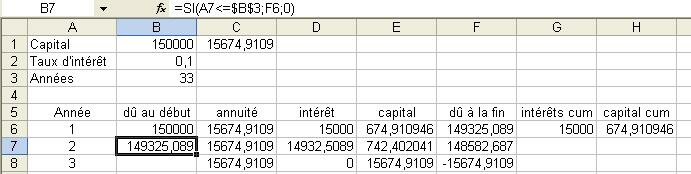
Pour calculer ce que vous devez en début d'année, vous devez indiquer une formule à avec une condition " SI ".
Comme ici, dans la cellule B7, on utilise SI (A7<=$B$3;F6;0).
Cette formulet veut dire :
Si, l'année qui se trouve dans la cellule A7 ou LC(-1) est inférieure ou égale à l'année se trouvant dans la colonne $B$3 (c'est-à-dire 30 ans ou 33 ans),
alors le montant à rembourser au début sera égal à ce qui se trouve dans la colonne F6 ou L(-1)C(+4),
si pas le montant à rembourser sera de 0 €.
Pourquoi dans la formule on retrouve le symbole $ ?
Car quand on met le symbole $, cela veut dire qu' on va utiliser pour toute la colonne le même montant. Dans ce cas, on a figé la formule B3, en figeant la ligne et la colonne et en écrivant $B$3.
On utilisera donc toujours "30 ans" (ou toute valeur introduite en B3) pour vérifier si l'on a pas dépassé la limite de temps de l'emprunt et calculer ce que l'on doit au début de chaque année (qui est ce que l'on devait en fin d'année précédente).
Le lecteur attentif aura remarqué qu'il aurait suffi de figer la ligne sans la colonne, puisque la copie s'est faite dans une même colonne. Écrire B$3 aurait été suffisant.
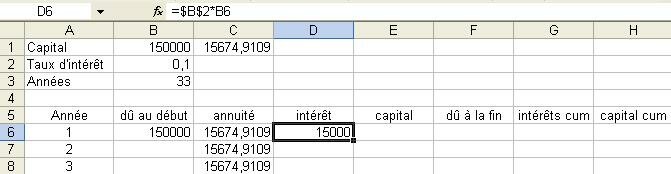
Pour calculer les intérêts à rembourser, on utilise la formule suivante =$B$2*B6.
Cette formule veut dire que l'on multiplie le taux d'intérêt par le montant dû au début de l'année.
On met des dollars entre B et 2, car le taux d'intérêt sera identique toutes les années,
tandis que le montant dû au début de chaque année sera différent => c'est pour cela qu'on ne met pas le symbole $ entre B et 6 (qu'Excel comprendra donc comme LC(-2) ).
La part de capital remboursée chaque année est la différence entre :
- l'annuité constante (calculée en C1,
et recopiée de C6 à C35 pour qu'Excel ne fasse qu'une seule fois le calcul)
- et le montant de l'intérêt à payer pour cette année-là
(calculé dans la colonne D).
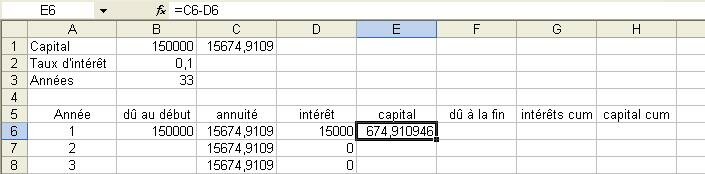
En E6, pour calculer le calculer le capital que l'on a à rembourser, on utilise la formule C6-D6.
Cela veut dire l'annuité (en LC(-2)) - les intérêts remboursés (en LC(-1)).
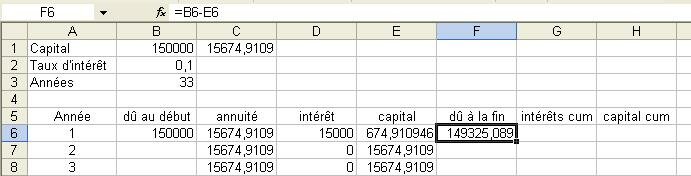
Pour savoir quel montant est dû à la fin, on emploie la formule suivante : B6-E6. Cela veut dire que l'on soustrait le montant dû au début de l'année avec capital et l'on obtient le montant dû à la fin.
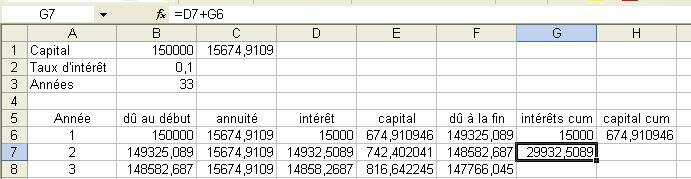
Pour les intérêts cumulés on additionne les intérêts de l'année en question avec les intérêts cumulés de l'année précédente.
Dans la formule à écrire en G7, on notera :
- les intérêts de l'année
(notés sur la même ligne 7, 3 colonnes plus à gauche [donc colonne D],
soit en D7)
- le signe "plus" ;
- les intérêts cumulés de l'année précédente
(notés sur la même colonne G, sur la ligne supérieure [donc ligne 6],
soit en G6)
Cette formule, située en G7, pourra être copiée dans la colonne G... jusqu'à la fin du tableau, puisque les adresses sont relatives.
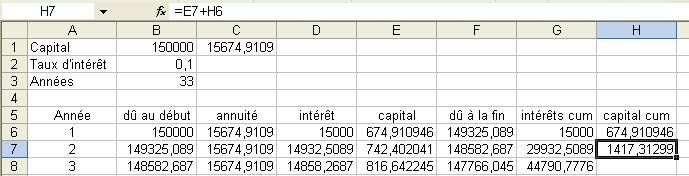
Pour le capital cumulé on additionne le capital remboursé de l'année en question avec le capital cumulé de l'année précédente.
Dans la formule à écrire en H7, on notera :
- le capital remboursé de l'année
(notés sur la même ligne 7, 3 colonnes plus à gauche [donc colonne E],
soit en E7)
- le signe "plus";
- le capital cumulé de l'année précédente
(notés sur la même colonne H, sur la ligne supérieure [donc ligne 6],
soit en H6)
Cette formule, située en H7, pourra être copiée dans la colonne H... jusqu'à la fin du tableau, puisque les adresses sont relatives.
Continuons sur notre lancée...
Si on changeait un peu l'énoncé !!
Au lieu de faire un prêt pour 30 ans, nous décidons de le faire en 33 ans.
Voilà ce que ça donne. Il vous suffit de changer dans la colonne B3 et de mettre 33 à la place de 30.
Ne changer rien d'autre !!
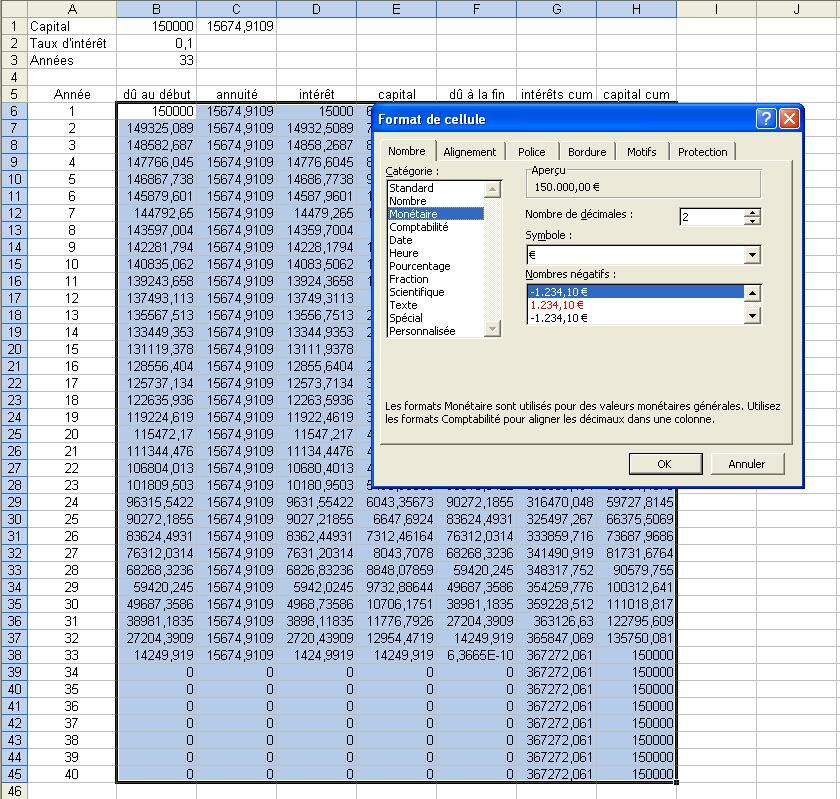
Vous avez emprunté 150 000 € et vous allez devoir rembourser 367 272,06 € ;
ce dernier montant est le prix que vous devez payer pour avoir emprunté une somme de 150 000 €.
C' est comme si vous payez le service du banquier. On parlera aussi de 'prix de la privation'.
Comment vérifier que le total du capital remboursé est bien 150 000 € ?
Comment vérifier que le total des intérêts payés est bien 367 272,06 € ?
Puisque la colonne D reprend pour chaque année, le montant annuel de l'intérêt payé, il suffirait de faire la somme de tous les montants de cette colonne.
Excel a prévu une fonction pour cela, il suffit d'employer la fonction =SOMME(champ à préciser) et le champ, dans ce cas-ci est l'ensemble des valeurs de D6 à D45... ce qui donne le même montant que la colonne G qui donne l'intérêt cumulé de toutes les années de remboursement.
De même, puisque la colonne E reprend pour chaque année, le montant annuel du capital remboursé, il suffirait de faire la somme de tous les montants de cette colonne.
Excel permet l'usage de la même fonction pour cela, il suffit d'employer la fonction =SOMME(champ à préciser) et le champ, dans ce cas-ci est l'ensemble des valeurs de E6 à E45... ce qui donne le même montant que la colonne H qui donne le capital remboursé cumulé de toutes les années de remboursement.
Compte tenu que la formule en D47 est la même que celle de E47, il suffit de faire un copier-coller de cette formule exprimée en adresse relative...
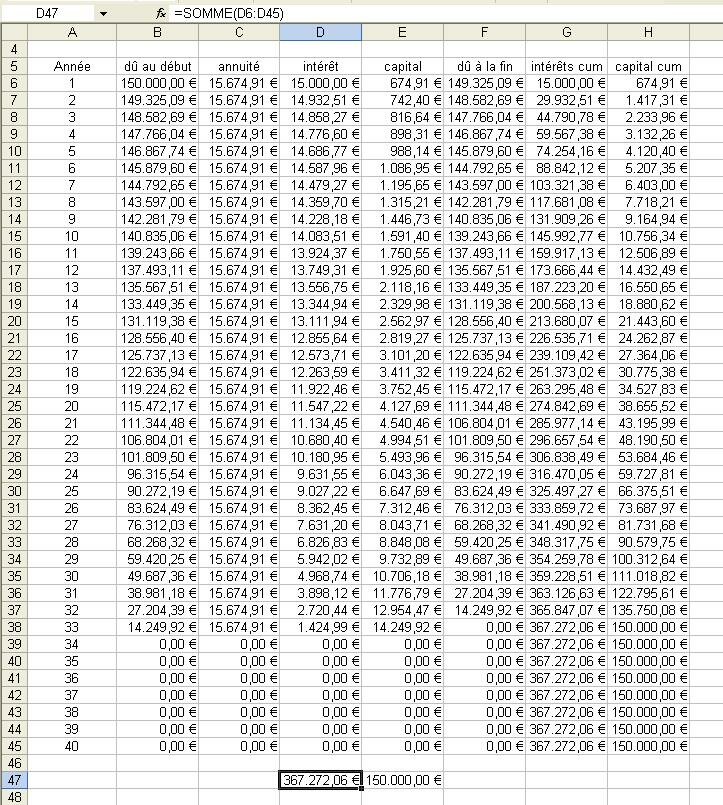
Pour améliorer la présentation et ne plus avoir un nombre variable de chiffres après la virgule, il suffit d'imposer un format à toutes les cellule du tableau... ou au moins à celle qui contiennent des montants calculés. Sélectionnez donc la zone de B6 à H47 et...
Ensuite vous allez dans :
format,
cellule,
nombre,
monétaire et
vous sélectionnez le symbole €.
Quel travail professionnel, pas vrai ?
Travail réalisé par Noussis Kathia 2NSSE
avec l'aide de Laetitia Hubrecht 2NSSE pour les captures d'écran.
|
Merci de votre visite à partir de : Vous êtes sur : https://cuy.be/cours/excel/kano_emprunt_excel.htm
|