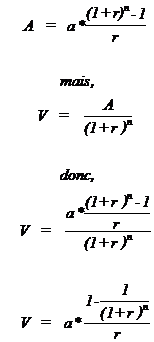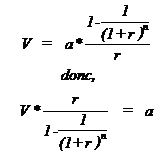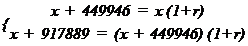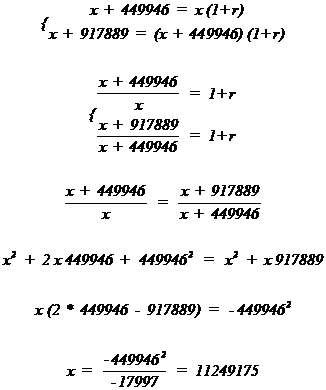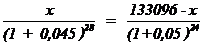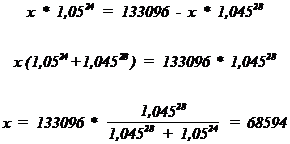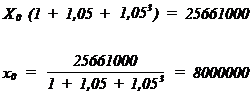Économie générale,
sociale
et politique
(ancien) Cours de Guy Van de Kelder
(ex-) Régendat math/sc.éco
École Normale Braine-le-Comte
♦ Sommaire, Introduction, Programmes et mots-clefs
♦ ÉCONOMIE = Comment lire ce syllabus ?
♦ Parabole de la veuve et des deux fils
♦ Une préparation type ?...Non ! (facture, note de débit, note de crédit)
♦ Et cette préparation est-elle type ? (indice et index)
♦ Algèbre financière : un sujet économique parmi d'autres...
♦ À retenir
♦ Exercices et Travaux
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent....
♦ Table des matières
|
♦ Sommaire, Introduction, Programmes et mots-clefs
|
-
Économie = ?
-
Contenu des étapes
-
Programmes de disciplines que vous êtes susceptibles de pouvoir enseigner
I. Économie = ?
= économistes : intendants du bonheur
= économie : que, comment et pour qui produire ?
= économistes : calculateurs froids, spécialistes de ce dont on ne parle pas même si on y pense toujours, voyants, prophètes, prévisionnistes...
II. Contenu des étapes
0
♦ Sommaire, Introduction, Programmes et mots-clefs
♦ ÉCONOMIE = Comment lire ce syllabus ?
♦ Parabole de la veuve et des deux fils
♦ Une préparation type ?...Non ! (facture, note de débit, note de crédit)
♦ Et cette préparation est-elle type ? (indice et index)
♦ Algèbre financière : un sujet économique parmi d'autres...
♦ À retenir
♦ Exercices et Travaux
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
1
♦ PREMIÈRE ÉTAPE : la famille Van Vlees dans l'Économie belge
♦ Introduction, objectifs et mots-clefs
♦ Science Économique et Sciences Sociales : leur objet ?
♦ D'où viennent nos besoins ? Ont-ils une origine sociale ? Pourquoi ?
♦ Rareté et travail : Pourquoi travaillons-nous ?
♦ Gestion des ressources rares : un des objets de l'économie
♦ Agents économiques et leurs principales opÉrations
♦ Circuit économique
♦ Exemple d'utilisation du circuit économique
♦ Secteurs institutionnels, acteurs économiques et leurs opérations économiques
♦ Processus productif : facteurs de production et rôle des entreprises dans leur combinaison
♦ Le circuit Économique : rappel et suite...
♦ à retenir
♦ Exercices et Travaux
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
2
♦ deuxième étape : monsieur Van Vlees au travail
♦ Introduction, objectifs et mots-clefs
♦ Qui est actif ? inactif ? Comment Évolue la population active ?
♦ Secteurs d'activité
♦ Professions et catégories socioprofessionnelles : PCS
♦ Le chômage
♦ Organisation du travail : Taylor, Ford, et après ?...
♦ Les relations sociales dans l'entreprise
♦ Un peu de droit sociall
♦ Cas particulier : enseignants de l’enseignement subventionné libre
♦ Les pouvoirs publics
♦ Les goupes intermédiaires
♦ Les fondements du pouvoir politique
♦ L'exercice de la démocratie et limitation du pouvoir politique
♦ Lieu du pouvoir politique et Organisation du pouvoir politique
♦ À r e t e n i r
♦ Exercices et travaux
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
3
♦ troisième étape : l'entreprise "Pacher" dans l'économie belge
♦ Introduction, objectifs et mots-clefs
♦ Les entreprises combinent travail et capital pour produire des richesses supplémentaires
♦ L'efficacité de la combinaison productive : productivité, progrès technique, innovation
♦ Le partage de la valeur ajoutée
♦ Les différentes formes juridiques
♦ Objectifs et principes de la comptabilité nationale
♦ Le tableau des entrées-sorties (TES ou I/O) et le calcul du PIB
♦ Du PIB au Revenu national : agrégats
♦ Comptes extérieurs : balances commerciale, des invisibles et des transactions courantes
♦ Les grands équilibres de l'économie
♦ Autre approche : La Bordurie
♦ Exemple d'utilisation de la Compta Nationale
♦ À retenir
♦ Exercices et travaux
♦ Voir aussi...
♦ Évaluation des connaissances et des savoir·faire
♦ Ce que les programmes en disent...
♦ Table des matières
4
♦ quatrième étape : M. Van Vlees gagne... Mme. Van Vlees dépense...
♦ Introduction, objectifs et mots‑clefs
♦ Première approche de la notion de revenu
♦ La distribution des revenus primaires
♦ La redistribution des revenus : les revenus de transferts
♦ Les inégalités de revenus
♦ Le crédit
♦ Le budget des ménages
♦ La notion de consommation et la diversité de consommation
♦ La mesure de la consommation
♦ L'évolution de la consommation des ménages
♦ Les consommations collectives
♦ Mode de vie, Niveau de vie
♦ À retenir...
♦ Exercices et Travaux
♦ Évaluation des savoirs et savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
5
♦ cinquième étape : M. Van Vlees et Mme. Van Vlees paient des impôts...
♦ Introduction, objectifs et mots-clefs...
♦ Trop d'état ? rage taxatoire et critique libérale
♦ Crise l'État-Providence et Politique de redistribution ?
♦ État producteur et privatisations
♦ La déréglementation et ses limites
♦ Le niveau de vie
♦ Le mode de vie
♦ Modes de vie et Styles de vie
♦ Peut-on orienter le choix du consommateur ?
♦ Qu'est-ce que la culture ?
♦ Les rapports interculturels
♦ La double nature de l'homme, biologique et sociale
♦ La production sociale de l'homme : la socialisation
♦ Qu'est-ce que la sociologie ?
♦ La sociologie & ses méthodes : application étude de la stratification
♦ Stratification sociale des sociIétés traditionnelles : castes et ordres
♦ Stratification sociale des sociétés traditionnelles : classes et catégories sociales
♦ À retenir...
♦ Exercices et travaux
♦ Ce que les programmes en disent...
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Table des matières
6
♦ sixième étape : M. Van Vlees et Mme. Van Vlees épargnent...
♦ Introduction, objectifs et mots-clefs
♦ L'épargne des ménages
♦ Le patrimoine des ménages
♦ Qu'est-ce que la monnaie ?
♦ Le banquier, un commerçant d'argent ?
♦ Le système bancaire et le financement indirect de l'économie
♦ Les marchés de capitaux et le financement direct de l'économie
♦ À retenir...
♦ Exercices et travaux
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
7
♦ septième étape : les Van Vlees dans une économie en mouvement...
♦ Introduction, objectifs et mots-clefs
♦ La famille, un phénomène social
♦ La famille dans la Belgique contemporaine
♦ La personnalité juridique
♦ Valeur, Normes et contrôle social
♦ L'exercice du contrôle social : l'exemple de la réaction sociale face à la délinquance
♦ L'évolution et la transformation des normes
♦ Qu'est-ce que l'opinion ?
♦ Comment connaître l'opinion ? Sondages, entretiens et enquêtes
♦ Peut-on faire l'opinion ? Les médias
♦ À retenir
♦ Exercices et travaux
♦ Évaluation des connaissances et savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
8
♦ huitième étape : le marché : royaume du consommateur et du producteur...
♦ Introduction, objectifs et mots-clefs
♦ La demande et l'offre : La détermination de l'Équilibre du marché
♦ LE MARCHÉ DE CONCURRENCE PURE ET PARFAITE
♦ De la concurrence parfaite à la concurrence imparfaite
♦ Le fonctionnement de la concurrence imparfaite
♦ Le rôle des prix
♦ Les limites du marché dans la satisfaction des besoins
♦ La production non marchande dans les pays développés
♦ Le marché : une construction historique
♦ Marché, organisations et institutions
♦ L'extension du marché et sa critique
♦ À retenir...
♦ Exercices et travaux
♦ Évaluation des connaissances et savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
9
♦ neuvième étape : la maîtrise de la machine économique...
♦ Introduction, objectifs et mots-clefs
♦ Les différentes fonctions de l'État : offre de services collectifs, redistribution, régulation
♦ Objectifs de la régulation conjoncturelle
♦ Politique de relance
♦ Politique de stabilisation
♦ Principaux moyens de l'intervention publique : budget, monnaie, protection sociale, secteur public et planification, réglementation
♦ Théories d’autres grands économistes
♦ À r e t e n i r
♦ Exercices et travaux
♦ Évaluation des connaissances et des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
♦ Table des matières
III. Programmes de disciplines que vous êtes susceptibles de pouvoir enseigner
|
1983 36 1B &2P 92 Méthodes de travail et d'études
1983 39 1B &2P 41 Travaux de bureau
1983 145 5&6 TT 67 sciences sociales et éducatives
1983 148 3 &4 QT 16 sciences humaines
1984 13 345 &6 QP 137 FormHumSocFamil
1984 14 345 &6 QP 111 questions d'actualités
1984 71 3 &4 T 8 form pratiq à la vie quotidienne
1985 23 3 &4 QT 151 éco : secrétar &bureautique
1985 25 3 &4 QT 245 éco : administration
1985 26 3 &4 QT 258 éco : distribution
1985 27 3 &4 QT 170 éco : accueil &tourisme
1986 16 123456 &7 76 informatique
1986 19 123456 &7 86 informatique
1986 20 345 &6 QP 227 fich 1 : quest d'actualités
1986 21 345 &6 QP 413 fich 1 : cours FHSF
1986 26 123456 &7 54 informatique, techniques nouvelles et civilisation
1986 30 5&6 QP 126 éco : monitorat d'accueil
1987 30 7 P 25 éco : auxiliaire en gestion de vente
1987 50 3 &4 QT 35 sciences humaines
1987 66 3 &4 QP 99 éco : travaux de bureau
1987 81 5&6 QT 129 sciences sociales appliquées
1987 88 5&6 QP 74 éco : vente, étalage
1987 93 5&6 QP 83 SAP : agents de collectivité
1987 98 345 &6 QP 51 fich 2 : quest d'actualités
1987 117 7 P 19 éducation économique et sociale
1987 132 7 P 22 éco : travaux de bureau
1987 133 7 P 32 éco : vente, étalage
1988 38 3 &4 QP 95 éco : vente, étalage
1988 51 5&6 QT 19 techniques publiciaires
1988 52 5&6 QP 82 éco : travaux de bureau
1988 60 7 P 80 éco : gestion et magasin
1989 72 3 &4 QT 121 éco : lg modern &bureautique
1989 76 345 &6 QT 16 informatique industrielle
|
1989 81 5&6 QP 178 SAP : moniteurs pour collectivités d'enfants
1990 14 3 &4 QT 116 éco : lg mod, rel publi
1990 42 345 &6 QP 143 fich 2 : cours FHSF
1991 46 1B &2P 400 Options groupées, formation de base
1991 56 3 &4 QT 123 éco : compta &informat de gestion
1991 68 5&6 QP 530 SAP : auxiliaire familiale et sanitaire
1991 78 7 P 48 arts appliq : conception et communication visuelle
1992 81 1&2 G 190 soc-éco : programme
1992 89 5&6 TT 67 sciences économiques appliquées
1992 102 123456 &7 134 informatique (atelier)
1992 127 1&2 G 420 soc-éco : mod 6
1992 128 1&2 G 240 soc-éco : mod 5
1992 129 1&2 G 260 soc-éco : mod 4
1992 130 1&2 G 180 soc-éco : mod 3
1992 131 1&2 G 260 soc-éco : mod 2
1992 132 1&2 G 140 soc-éco : mod 1
1993 17 3 &4 QT 213 serv aux pers : techniques sociales
1993 30 5&6 QT 190 techniques sociales
1993 31 123456 &7 170 éducation à la sécurité
1994 16 3 &4 T 244 sc éco, O.B. 4p
1994 23 3 &4 QT 220 éco : secrétariat
1994 24 7 P 60 aménagement de l'espace rural
1994 27 3 &4 QT 235 éco : gestion
1994 30 3 &4 QP 286 serv aux pers : services sociaux
1995 105 345 &6 T 505 sc soc, O.B., doc accomp 1
1995 116 123456 &7 54 éducation à la santé
1995 123 345 &6 T 76 sc soc, O.B., 4p
1995 125 3 &4 TT 172 sciences sociales et éducatives
1996 3 5&6 QT 102 connaissances de gestion
1996 38 123456 &7 141 éducation à l'expression
1996 44 345 &6 T 838 sc soc, O.B., doc accomp 2
1997 7 3456 QT &P 154 sciences humaines
1997 21 7 P 269 agronomie : gestion des entreprises
9900000388 1&2 G 1400 soc-éco : mod (série complète)
SCEC 94 3 &4 TT 251 sciences économiques appliquées
SDAF S92 5&6 QP 220 SAP : déontologie
|
|
♦ ÉCONOMIE = Comment lire ce syllabus ?
|
-
Orientation générale
-
Les règles de lecture des étapes des premiers pas en économie
-
Quelques conseils complémentaires...
La suite de l'ouvrage que nous vous présentons n'a pas la prétention de remplacer un manuel d'économie pour l'enseignement secondaire ou supérieur de type court, ni même d'être un ouvrage d'initiation économique. Il est une compilation d'ouvrages divers dont nous ne pourrions citer toutes les sources et dont nous voudrions seulement faciliter la lecture pour les jeunes ou les personnes ne possédant pas une culture économique élémentaire.
I. Orientation générale
L'orientation générale de l'ouvrage est la suivante : présenter les données de base dans une approche globale de l'économie permettant de les situer les unes par rapport aux autres. Par ailleurs, la représentation graphique des relations économiques fondamentales facilite leur compréhension.
Par contre, la méthode est très particulière. Tandis que beaucoup d'ouvrages s'adressent à ceux qui, par leur engagement ou leur formation possèdent déjà une culture économique de base, qu'il s'agit d'exploiter et d'élargir afin de parvenir à une synthèse personnelle, le présent document est axétant sur l'acquisition de ces données de base que sur leur approfondissement.
Toutefois, dans une première approche, il ne tend nullement à les faire découvrir à partir d'observations et de connaissances encore mal maîtrisées. En effet, tout le monde fait de l'économie sans le savoir, et le but de ces premiers pas en économie est d'amener le lecteur à comprendre la signification économique de ses actes. L'enseignement programmé, qui a inspiréla méthode employée dans cet ouvrage, pour la première approche, correspond parfaitement à cette démarche. Les professeurs doivent y retrouver une méthode qu'ils peuvent employer : celle de la pédagogie active qui invite les élèves à découvrir par eux-mêmes les notions à propos desquelles le professeur leur proposera une synthèse. L'enseignement programméne constitue qu'un support technique permettant de systématiser une ancienne méthode pédagogique.
Il obéit à quatre principes :
1. Principe des petits pas
2. Principe de la participation active
3. Principe de la vérification immédiate
4. Principe de l'allure personnelle.
Nous avons respecté ces principes tout en les aménageant en fonction des caractéristiques de l'économie et des contraintes de l'ouvrage édité. Aussi avons-nous préféré le terme d' "enseignement semi-programmé" à celui d' "enseignement programmé" auquel nous avons été le plus fidèle possible. En effet :
= Le lecteur est invité à ne faire qu'un pas après l'autre. Une notion nouvelle n'est présentée que lorsque tous les éléments nécessaires à sa compréhension ont été déjà analysés. La programmation utilisée est linéaire. Une programmation non linéaire aurait supposé un ouvrage d'une taille trop importante et peu maniable par le jeune lecteur.
= À chaque pas, le lecteur est invité à découvrir par lui-même les mots et les chiffres-clés. Il doit faire appel à des connaissances acquises quotidiennement ou dans les pages précédentes de l'ouvrage. Il sera ainsi amené à résoudre quelques petits problèmes, à jouer au jeu des estimations, ou encore à réaliser des graphiques de synthèse. Toutefois, nous n'avons pas poussé la programmation jusqu'à la suppression de tout texte de synthèse. L'économie est en effet inséparable d'une vie sociale où les rapports de forces interfèrent avec la logique et où l'option politique ne peut être négligée. Aussi avons-nous divisé l'ouvrage en grandes étapes, chaque étape en plusieurs ensembles se terminant chacun par un relais qui reprend dans la forme traditionnelle du discours l'essentiel de l'acquis, propose éventuellement un jugement et permet le passage à l'ensemble suivant.
= La vérification immédiate est réalisée par une correction qui se trouve sous le texte lacunaire. Cachée, elle devrait être progressivement dévoilée grâce à une feuille mobile. Nous n'avons pas voulu employer le système des deux livres qui aurait considérablement augmentéle prix de l'édition. Normalement, il n'existe qu'une réponse aux questions précises ; toutefois, comme les jugements peuvent diverger, il arrive que les réponses soient multiples. Dans ce cas, nous donnons dans la correction l'explication de nos choix.
= Le principe de l'allure personnelle a été le plus difficile à respecter. On ne peut parvenir à personnaliser l'allure du lecteur qu'en fonction d'une connaissance précise du milieu social et de la psychologie de ce dernier. L'animateur ou le professeur qui se servira de l'ouvrage doit donc éventuellement se charger d'une adaptation plus précise. Cependant, nous attirons sur quelques points l'attention des lecteurs isolés ou des jeunes qui voudraient réviser personnellement les notions de base. Nous avons commencé l'approche de l'économie à un niveau extrêmement bas. Que les lecteurs "normaux" ne s'étonnent pas du caractère presque enfantin des premières pages. L'expérience nous a montré qu'en initiation on peut aller très haut à condition de ne pas hésiter à être élémentaire au départ.
À côté des réponses, entre parenthèses, nous avons cité les numéros des paragraphes où le lecteur est renvoyé s'il se trompe. À la fin de chaque étape, nous avons placé la liste des notions étudiées au cours de celle-ci. Si l'une d'entre elles n'est pas comprise, le lecteur doit revoir les paragraphes indiqués. Après chaque relais, nous avons placé un test de progression ; c'est une question de synthèse qui doit permettre de fixer la compréhension générale du phénomène étudié.
Par ailleurs, nous conseillons au lecteur de ne pas étudier plus d'un ou deux ensembles par jour et, s'il a rencontré de réelles difficultés, de relire l'ensemble précédent avant de passer au suivant.
Au total, nous avons donc essayé de créer un instrument permettant à des jeunes aussi bien qu'à des adultes ne possédant pas une culture économique élémentaire de comprendre et d'assimiler les notions économiques de base. Pour ces dernières, comme nous l'avons déjà dit, cet instrument ne remplace ni le manuel ni le professeur. Il peut faciliter la compréhension d'ouvrages plus classiques, plus complets, mais prisonniers d'un programme, et aider au rattrapage de certains retards.
Dans une seconde approche, nous avons voulu aborder la même matière avec une approche plus structurée et plus complète. Deux objectifs ont été poursuivis dans cette seconde approche :
= rendre plus facile le travail personnel de l'étudiant, qui pourra y trouver des définitions précises, des résumés, des exemples illustrant le contenu et des invitations à utiliser les travaux et exercices que nous proposons en troisième approche ;
= répondre à un souhait de "professionnels de l'enseignement" en proposant des utilisations diverses de l'outil. Point de départ à une réflexion, il pourra jouer le rôle de document ; aide au travail relatif aux travaux et exercices proposés en troisième approche, il structurera les notions qui y sont abordées ; source complémentaire, il pourra soit approfondir des notions insuffisamment traitées au niveau du cours, ou éventuellement s'y substituer.
Dans une troisième approche, nous souhaitons proposer une série de pistes méthodologiques et de matériel exploitable au niveau d'un cours à donner sur les sujets abordés. Ces documents invitent l'utilisateur à en faire usage non seulement pour s'initier progressivement à la discipline économique au travers de documents divers (extraits de romans, d'études, de statistiques, de bandes dessinées, etc.), mais également pour illustrer ou mettre en oeuvre des notions abordées par ailleurs, et même pour évaluer les connaissances et savoir-faire à mettre en place. Nous informons le lecteur que ces outils proposés sont parfois d'un niveau trop difficile pour une exploitation dans le secondaire inférieur, mais ils offrent l'avantage de voir le sujet économique d'une autre manière que la voie classique.
Dans une dernière approche, nous souhaiterions aussi porter à la connaissance du lecteur d'autres ouvrages, compléments d'informations, films et autres qui traitent des mêmes sujets ("À voir aussi...") et nous voudrions y intégrer aussi les références aux programmes du secondaire, relatives aux sujets traités ("Ce que les programmes en disent...")
De ce fait, ce livre ne s'adresse pas à une classe en particulier. Toutefois, son contenu le destine plus spécialement aux futurs enseignants en économie. Il est né d'une expérience de pédagogie active réalisée tant dans un milieu de jeunes que dans un milieu d'adultes et il a été testé à partir de groupes fort divers.
Nous ne pensons pas cependant être parvenu à lui donner une forme parfaitement satisfaisante ; aussi serions-nous reconnaissant à tous ceux qui l'utiliseront de nous envoyer leurs réflexions et de nous dire bien simplement les difficultés qu'ils ont rencontrées dans son utilisation.
Toute activité, réalisée ou simplement suggérée, pourrait venir augmenter notre réserve de "travaux". Un jeu, un film, un programme informatique interactif pourraient permettre de compléter la formation donnée par cet ouvrage en essayant d'affronter le lecteur aux choix économiques fondamentaux.
II. Les règles de lecture des étapes des premiers pas en économie
01.= Lire le premier "paragraphe" lacunaire (numéroté en chiffre romain) de l' "étape", et écrire les mots manquants ou répondre aux questions en se servant d'un crayon afin de pouvoir gommer les erreurs.
02.= Baisser votre "cache", si les réponses se trouvent sur la même feuille, et vérifier sa réponse. En cas d'erreur, retourner aux paragraphes indiqués au bas de la réponse. Si le paragraphe est trop long, répondre par toutes petites étapes et baisser progressivement le cache.
03.= Passer ensuite au paragraphe suivant.
04.= Tous les paragraphes terminés, passer ensuite à la lecture du "relais", texte non lacunaire résumant les paragraphes de l'étape.
05.= Si l'on ne comprend pas un relais, revoir la série de paragraphes qui l'introduisent.
06.= Faire de même pour le test de progression, mais, de plus, relire le relais.
07.= Après le test de progression, on peut passer au texte lacunaire des paragraphes suivants.
08.= Après chaque étape, on trouvera une liste des notions acquises dans les ensembles qui la composent. Si l'une de ces notions demeure obscure, revoir le paragraphe (ou l'ensemble) qui s'y rapporte.
09.= Après la liste des notions acquises lors de chaque étape, on trouvera des notions complémentaires à celles-ci. Cependant, le lecteur "pressé" pourrait ne pas approfondir ces notions, tout en comprenant l'essentiel vu lors de l'étape.
10.= Après les notions complémentaires, le lecteur trouvera l'essentiel à retenir de celles-ci. Ici, le lecteur "pressé" est invité à prendre connaissance de ces notions, pour comprendre l'essentiel de ce complément de formation de l'étape.
11.= Enfin, après l'essentiel à retenir des notions complémentaires, le lecteur trouvera des travaux et exercices permettant d'aborder ces notions l'essentiel à retenir de celles-ci. Ici, le lecteur "pressé" est invité à prendre connaissance de ces notions, pour comprendre l'essentiel de ce complément de formation de l'étape.
12.= À la fin de chaque étape, le lecteur pourra trouver une évaluation de ses connaissances et savoir-faire (sans solution) qui lui permettront de s'autoévaluer.
13.= Avant une table des matières, le lecteur pourra s'informer d'autres sources qui pourraient compléter son information et la manière de présenter le sujet au niveau de cours. Il y verra notamment un aperçu des programmes qui proposent ces matières à voir.
III.Quelques conseils complémentaires...
Ce syllabus ne doit pas être lu d'un seul trait : vous ne devez en lire qu'un ensemble par jour, au besoin deux, très rarement trois. Si vous avez des difficultés :
1) ne lisez qu'un ensemble sans faire le test de progression ;
2) le jour suivant, relisez le relais étudié la veille et faites le test de progression ;
3) passez seulement ensuite à l'ensemble suivant.
Ne vous découragez pas si vous faites des erreurs. L'erreur n'est pas grave lorsqu'on peut la corriger et en comprendre la cause.
Le jeu de l'évaluation vous offre la possibilité de vérifier l'exactitude de certaines de vos estimations. Parfois, celles qui vous seront demandées vous paraîtront trop difficiles. En fait, il ne s'agit pas d'exiger de votre part la connaissance de chiffres d'une parfaite précision mais plutôt, grâce à la confrontation de votre opinion et de la réalité, de graver dans votre mémoire certains ordres de grandeur qu'il est indispensable de connaître pour avoir une vue saine de la vie économique.
La réponse à certaines questions est souvent plus ample que celle que vous pouvez formuler. Nous l'avons fait pour vous faciliter leur compréhension. Ne vous effrayez pas si vous avez été plus bref, seul importe le sens de votre réponse.
|
♦ Parabole de la veuve et des deux fils[1]
|
-
Les personnages
-
Les maths et l'économie
-
Et la concurrence ?
-
Le droit et l'économie
-
Les notions abordées
I. Les personnages
Désolé pour l'aspect mathématique de cette approche, mais cette approche allie méthodologie, approche scientifique et interdisciplinarité des disciplines…
Une mère (m) a une exploitation agricole, seule ressource de la famille, deux fils et un seul outil. L'un des fils est fort (F), grand et costaud ; l'autre (f) chétif et faiblard. La durée totale possible de travail est de 12 heures par jour, nous la noterons H ci-après ; l'outil étant unique, il conviendra de partager les heures de travail entre F et f.
Le souci de la mère est d'assurer le bonheur familial, la survie de ses enfants, et, accessoirement, sa propre survie. Deux variantes pourront donc être suivies.
-
Hypothèse 1 : partage de l'outil, chacun mange sa production
-
Hypothèse 1, variante
-
Hypothèse 2 : emploi de l'outil selon sa consommation
A. Hypothèse 1 : partage de l'outil, chacun mange sa production
Le fort produit naturellement plus que le faible pendant ses 6 heures de travail ; mais, comme il se dépense plus, il a droit à manger plus.
La mère est heureuse, mais ne consomme rien.
Nous noterons H le nombre d'heures de travail de chacun, P la quantité produite par chacun et C, la consommation de chacun ; les indices m, F et f désigneront respectivement la mère, le plus fort et le plus faible des enfants.
|
HF = 6
|
|
Hf = 6
|
|
H = 12
|
|
PF = 180
|
|
Pf = 108
|
|
P = 288
|
|
CF = 180
|
|
Cf = 108
|
|
C = 288
|
B. Hypothèse 1, variante
et la mère ? // chacun la moitié ? // et si le minimum vital est de 80 unités ? // et si le costaud participait plus ?
1. et la mère ?
Pour sa survie, la mère ne peut se contenter du seul bonheur de ses fils. Dans l'impossibilité de participer au travail, il est convenu que chacun contribue à l'alimentation de la mère.
Le problème : quelle sera la contribution ? Situation identique, ne tenant pas compte de la mère :
|
HF = 6
|
|
Hf = 6
|
|
Hm = 0
|
|
H = 12
|
|
PF = 180
|
|
Pf = 108
|
|
Pm = 0
|
|
P = 288
|
|
CF = 180
|
|
Cf = 108
|
|
Cm = 0
|
|
C = 288
|
2. chacun la moitié ?
La contribution sera identique, soit de chacun 20 unités produites.
|
HF = 6
|
|
Hf = 6
|
|
Hm = 0
|
|
H = 12
|
|
PF = 180
|
|
Pf = 108
|
|
Pm = 0
|
|
P = 288
|
|
CF = 160
|
|
Cf = 88
|
|
Cm = 40
|
|
C = 288
|
3. et si le minimum vital est de 80 unités ?
La production totale étant de 288, elle suffit à nourrir tout le monde ; cependant une contribution identique, soit de chacun 40 unités produites permet la survie de la mère mais plus celle du faible, qui passe sous le minimum vital.
|
HF = 6
|
|
Hf = 6
|
|
Hm = 0
|
|
H = 12
|
|
PF = 180
|
|
Pf = 108
|
|
Pm = 0
|
|
P = 288
|
|
CF = 140
|
|
Cf = 68
|
|
Cm = 80
|
|
C = 288
|
4. et si le costaud participait plus ?
La production totale étant de 288 et le minimum vital de 80 unités, il suffit que le faible donne selon ses possibilités et le costaud, le reste ; cependant une telle contribution semblera injuste, car exagérée et disproportionnée, aux yeux de ce dernier.
|
HF = 6
|
|
Hf = 6
|
|
Hm = 0
|
|
H = 12
|
|
PF = 180
|
|
Pf = 108
|
|
Pm = 0
|
|
P = 288
|
|
CF = 128
|
|
Cf = 80
|
|
Cm = 80
|
|
C = 288
|
Quelle sera la réaction du plus fort qui estimera que ce n'est pas juste qu'il doive donner plus que son frère ?
C. Hypothèse 2 : emploi de l'outil selon sa consommation
Le fort produit naturellement plus que le faible ; mais, comme il produit plus que ce dont il a besoin, il décidera probablement de réduire son temps de travail.
On peut imaginer que, travaillant une heure en moins, le costaud ressentira moins les effets de la fatigue et que le rendement de ses heures de travail sera meilleur ; par contre celui du faiblard diminuera.
|
HF = 5
|
|
Hf = 7
|
|
H = 12
|
|
PF = 155
|
|
Pf = 112
|
|
P = 267
|
|
CF = 155
|
|
Cf = 112
|
|
C = 267
|
On constate que la production globale diminue ; quant à la contribution à la survie de la mère, le problème reste posé. De plus, le costaud pourrait encore travailler moins, tout en parvenant à subsister, ce qui entraînerait une surcharge de travail pour le faible. Remarquons qu'une heure supplémentaire de travail pour le faible ne lui a pas apportéune grande augmentation de production.
À partir de cette hypothèse, il nous est permis de poser les mêmes variantes que ci-dessus, à savoir le problème de survie de la mère. Remarquons aussi que, si le minimum vital avait été fixé à 90 unités, au lieu de 80, la production globale ne suffirait plus à nourrir tout le monde.
Le lecteur pourrait à juste titre se demander si les chiffres donnés ci-dessus sont farfelus, ou s'ils émanent d'une mure réflexion. La suite répondra à cette question : ils émanent d'un modèle économique inventé de toutes pièces et dont voici quelques éléments de base :
II. Les maths et l'économie
-
Le modèle : sa construction
-
Le modèle : son utilisation pour une production optimale
A. Le modèle : sa construction
Les chiffres donnés ci-dessus peuvent paraître farfelus et arbitraires. Comment un enseignant peut-il "inventer" des chiffres et justifier son choix. Excellente occasion d'associer nos connaissances en math et en économie. Efforçons-nous de trouver nous-mêmes un modèle qui explique la production (P) par le nombre d'heures de travail (H) ; c-à-d où P = f(H).
= il faut H=0 ==> P=0 ;
ou pas de production si on ne travaille pas ;
= il faut si H augmente ==> P augmente ;
ou P est une fonction croissante par rapport à H ;
ou P' > 0 ; car une fonction est croissante
==> sa dérivée première est positive ;
ou plus je travaille, plus ma production augmente
(jusqu'à une certaine limite) ;
= il faut H augmente ==> P augmente de moins en moins vite ;
ou P est une fonction croissante par rapport à H,
mais à croissance de - en - rapide ;
ou P"< 0 ;
car la concavité vers les y négatifs donc, sa dérivée seconde négative ;
ou plus je travaille, plus je me fatigue
et moins ma production augmente
(jusqu'à un certain épuisement) ;
La portion croissante d'une parabole à maximum, donc à concavité vers le bas répondrait à ces critères :
P = a H2 + b H + c
avec,
P' = 2 a H + b
et,
P"= 2 a
* il faut
c = 0
* il faut aussi
a <0
* il faut également
2 a H + b >0
* de plus
P max, si P'=0 ou si H*= - b (0« H* <24)
2a
Idéalement H* » 0 ; or, a <0, donc -b <0 et donc b >0
avec H* représentant le nombre d'heures de travail pour avoir une production maximale
Ces observations étant valables d'une manière générale pour toute production dépendant des prestations, nous nous trouvons ici en présence de 2 fonctions, à savoir les productions des 2 frères.
PF = aF HF2 + bF HF + cF
et
Pf = af Hf2 + bf Hf + cf
c = 0, d'où
PF = aF HF2 + bF HF
et
Pf = af Hf2 + bf Hf
Si nous considérons que le fort atteindra un maximum de production après 18 heures et le faible après 7,5 heures, on aura :
H*F = -bF / 2 aF = 18 ==> -bF = 36 aF
et
H*f = -bf / 2 af = 7,5 ==> -bf = 15 af
De plus, nous savons qu'en travaillant chacun 6 heures, ils produisent respectivement 180 et 108 unités, on aura :
180 = aF 6 + bF 6
et
108 = af 6 + bf 6
d'où,
180 = aF 62 - 36 aF 6 = 36 aF (1-6)
et
108 = af 62 - 15 af 6 = 6 af (6-15)
d'où
aF = 180 / (-180) =_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ -1
et
af = 108 / (-54) =_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ -2
ce qui vérifie la nécessité de a<0 ;
dès lors,
bF = 36
et
bf = 30
ce qui vérifie la nécessitéde b>0 ;
Les fonctions de production respectives sont donc :
PF = -1 HF2 + 36 HF
et
Pf = -2 Hf2 + 30 Hf
Ces fonctions de production pourraient être traduites dans le tableau de chiffres suivant :
|
heures de travail
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
production du fort
|
0
|
35
|
68
|
99
|
128
|
155
|
180
|
203
|
224
|
243
|
260
|
|
production du faible
|
0
|
28
|
52
|
72
|
88
|
100
|
108
|
112
|
112
|
108
|
100
|
Ce qui est le reflet des fonctions données ci-avant,
puisque pour 6 heures de travail, le fort produisait 180 unités et le faible 108 unités
B. Le modèle : son utilisation pour une production optimale
hypothèse 3 :repartition pour production optimale // production maximale // retenues optimisées
1. Hypothèse 3 : répartition pour production maximale
Un futur Régent en math/sciences éco de Braine-le-Comte arrive et déclare qu'il doit être possible de trouver alors la production maximale, tenant compte de la présence d'un seul outil et d'une durée de travail de 12h au total, il conclut que le faible ne pourra prester que le temps non utilisé par son grand frère (jusque là, pas d'invention exceptionnelle).
Il suffira dès lors d'optimiser la production totale, qui ne sera rien d'autre que la somme des 2 productions individuelles, en dérivant cette fonction de production par rapport à la variable "heures de travail". Et, si l'on oublie pas que Hf = (12-HF), on aura :
PF = -1 HF2 + 36 HF
et
Pf = -2 (12-HF)2 + 30 (12-HF)
Donc,
P = -1 HF2 + 36 HF + [ -2 (12-HF)2 + 30 (12-HF) ]
ou,
P = -1 HF2 + 36 HF -2 (144- 24 HF + HF2) + 30 (12-HF)
ou,
P = -1 HF2 + 36 HF -288 +48 HF -2 HF2 + 360 - 30 HF
ou,
P = -3 HF2 + 54 HF + 72
Dont la dérivée première est :
P' = [ -3 HF2 + 54 HF + 72 ]' = -6 HF + 54
P sera optimale lorsque sa dérivée première s'annulera, donc si :
-6 HF + 54 = 0 ==> HF = 9
ç.-à-d. lorsque le fort travaille 9 heures (ou 18 demi-heures pour les non matheux ! !) et le faible 3
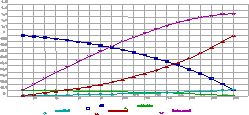
La production cumulée (somme de celle du fort et du faible) pourra dès lors se représenter comme suit :
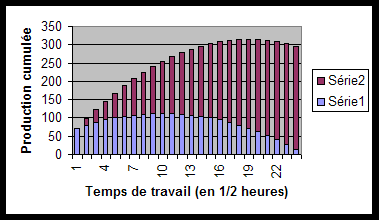
2. Production maximale
Le lecteur emploiera les fonctions ci-dessus pour déterminer les valeurs suivantes qui maximalisent la production totale en se répartissant les 12 heures de travail possible, si l'on garde l'hypothèse que chacun consomme ce qu'il a produit et que la mère ne vit que du bonheur de ses enfants :
|
HF = 9
|
|
Hf = 3
|
|
Hm = 0
|
|
H = 12
|
|
PF = 243
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 315
|
|
CF = 243
|
|
Cf = 72
|
|
Cm = 0
|
|
C = 315
|
3. Retenues optimisées
Pour permettre à chacun de pouvoir consommer le minimum vital (fixé arbitrairement à 80), le costaud subira une ponction de 80 + 8 soit 88, à distribuer à la mère et au faiblard.
|
HF = 9
|
|
Hf = 3
|
|
Hm = 0
|
|
H = 12
|
|
PF = 243
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 315
|
|
CF = 155
|
|
Cf = 80
|
|
Cm = 80
|
|
C = 315
|
Remarquons que, malgréune ponction supérieure, la part de revenu disponible du costaud est supérieure à celle disponible dans l'hypothèse de partage du travail (voir II.C.4.).
La mère ayant accepté, elle a fait le choix de critères différents pour la production (l'efficacité), et pour la consommation (répartition équitable aux yeux de la mère). Si le souffreteux avait pu ouvrir son coeur, on pourrait peut-être entendre : "Cela me gêne de manger ce qu'un autre à gagner, je veux travailler plus, vivre de mon travail, cesser d'être un assisté."
III. Et la concurrence ?
-
Présentation
-
Si la mère refuse...
-
Si la mère accepte...
-
Si le costaud exige plus, voire tout...
A. Présentation
Pas loin de là vivent un veuf Cornélius, et sa fille, malade également. "Cornélius me propose d'aller travailler pour lui, pour remplacer son valet qu'il a renvoyé. Je travaillerai 9 heures comme ici, mais il ne me prendra que 70 unités pour nourrir sa famille, au lieu des 88 que tu me prends. Je veux bien rester si tu ne me prends plus que 70 unités."
B. Si la mère refuse...
Seul le malingre devra se nourrir (et intervenir pour nourrir sa mère). Bien vite, il apparaîtra que le petit ne peut travailler les 12 heures (remarquons aussi qu'avec 12 heures de travail du faiblard, la production est la même qu'avec 3 heures). Le travail presté chez Cornélius n'intéresse pas la mère qui ne doit pas se soucier du costaud, qui vivra mieux qu'à la maison, d'où,
|
HF = 0
|
|
Hf = 12
|
|
Hm = 0
|
|
H = 12
|
|
PF = 0
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 72
|
|
CF = 0
|
|
Cf = 72
|
|
Cm = 0
|
|
C = 72
|
Mais, tenant compte des fonctions de production développées ci-avant, le lecteur se rappellera que le maximum de production du plus faible, est atteint après 7,5 heures, d'où :
|
HF = 0
|
|
Hf = 7,5
|
|
Hm = 0
|
|
H = 7,5
|
|
PF = 0
|
|
Pf = 112,5
|
|
Pm = 0
|
|
P = 112,5
|
|
CF = 0
|
|
Cf = 112,5
|
|
Cm = 0
|
|
C = 112,5
|
Et quelle que soit la forme de redistribution, on constatera que le minimum vital ne pourra pas être atteint pour la famille (réduite à 2 personnes et production maximale de 112,5).
C. Si la mère accepte...
Le lecteur constatera que la mère n'a pas le choix, en acceptant de limiter sa ponction à 70 au lieu des 88, la mère et son protégé bénéficieront des 72 produits en 3 heures de travail du plus faible, augmentés de 70, prélevés du travail du grand frère, soit une consommation de 142 pour 2 (soit 71 chacun), en lieu et place des 112,5 en cas de refus.
|
HF = 9
|
|
Hf = 3
|
|
Hm = 0
|
|
H = 12
|
|
PF = 243
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 315
|
|
CF = 173
|
|
Cf = 71
|
|
Cm = 71
|
|
C = 315
|
Accepter ce que propose le plus fort, c'est aussi accepter que "C'est toujours la misère, mais une misère moins grande."
D. Si le costaud exige plus, voire tout...
Le lecteur constatera que la mère n'a pas beaucoup d'arguments à développer si le costaud refuse des ponctions trop fortes, menaçant d'aller travailler chez Cornélius.
Situation extrême, le costaud travaille les 12 heures et garde toute sa production pour sa consommation propre, sans aucun partage.
|
HF = 12
|
|
Hf = 0
|
|
Hm = 0
|
|
H = 12
|
|
PF = 288
|
|
Pf = 0
|
|
Pm = 0
|
|
P = 288
|
|
CF = 288
|
|
Cf = 0
|
|
Cm = 0
|
|
C = 288
|
Remarquons que, par son seul travail, le fort pourrait subvenir aux besoins de tous, même si la production n'est pas optimale. De plus, le hasard des chiffres montre que la production est identique si le fort travaille 12 heures, ou si chacun travaille 6 heures.
IV. Le droit et l'économie
-
Les revenus de la propriété
3 heures à 10 unités, soit 30 unités // 3 heures à 40 unités, soit 120 unités // 3 heures à 16 unité, soit 48 unités // et si le petit bénéficiait d'un autre quota d'heures// quid le Cornélius et son outil inutilisé ?
A. Les revenus de la propriété
Un autre futur Régent en math/sciences éco de Braine-le-Comte, plus spécialiséen droit, arrive et déclare qu'il n'est pas normal que le fort puisse s'approprier de l'unique outil héritédu père, pendant toute la journée. Il doit être possible pour le malingre de trouver un prix de location optimal ; ni trop élevépour ne pas décourager le fort de louer l'engin et d'y gagner encore ; pas trop faible pour éviter que le faible n'y gagne pas assez. Il conclut que chacun ne pourra utiliser l'outil au delà de la moitiédu temps, que moyennant paiement d'un loyer à son frère.
Nous garderons l'hypothèse de la production optimale, atteinte lorsque le costaud travaille 9 h, son frère 3 h. Nous négligerons volontairement le problème de la ponction (fiscale) pour la survie de la mère, dans le but de mieux isoler le problème présenté.
1. 3 heures à 10 unités/heure, soit 30 unités ?
|
HF = 9
|
|
Hf = 3
|
|
Hm = 0
|
|
H = 12
|
|
PF = 243
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 315
|
|
CF = 243-30
= 213
|
|
Cf = 72+30
= 102
|
|
Cm = 0
|
|
C = 315
|
Le lecteur constatera que cette location de l'outil permet à chacun de consommer suffisamment, même si la situation de la mère reste à améliorer, l'intervention sera plus équilibrée.
Le costaud peut consommer 213 unités (avant retenue et/ou contribution), alors qu'au départ, en travaillant 6 h, il ne pouvait que consommer 180 unités : il n'hésitera pas à louer l'outil...à ce prix-là.
2. 3 heures à 40 unités/heure, soit 120 unités ?
|
HF = 9
|
|
Hf = 3
|
|
Hm = 0
|
|
H = 12
|
|
PF = 243
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 315
|
|
CF = 243-120
= 123
|
|
Cf = 72+120
= 192
|
|
Cm = 0
|
|
C = 315
|
Le lecteur constatera que cette location de l'outil permet non seulement à chacun de consommer suffisamment, mais permet au faible de consommer plus que le fort ; ici aussi, la situation de la mère reste à améliorer.
Il semble cependant peu probable que le fort accepte ce marché, sa consommation possible à ce prix étant inférieure à celle possible en ne travaillant que 6 h.
3. 3 heures à 16 unités/heure, soit 48 unités ?
|
HF = 9
|
|
Hf = 3
|
|
Hm = 0
|
|
H = 12
|
|
PF = 243
|
|
Pf = 72
|
|
Pm = 0
|
|
P = 315
|
|
CF = 243-48
= 195
|
|
Cf = 72+48
= 120
|
|
Cm = 0
|
|
C = 315
|
Ici encore, on constatera que le fort sera toujours d'accord de payer, puisqu'en n'employant l'outil que 6 heures, il récolte 180 unités, tandis qu'en louant pour 48 unités, il en produit 63 de plus et peut en garder 15.
Le lecteur constatera que cette location de l'outil permet au fort d'y gagner (15 unités) et au faible de consommer plus (12 unités) qu'en travaillant 6 heures ; de plus, si l'on imagine une heure de location en plus, on arriverait à :
|
HF = 10
|
|
Hf = 2
|
|
Hm = 0
|
|
H = 12
|
|
PF = 260
|
|
Pf = 52
|
|
Pm = 0
|
|
P = 312
|
|
CF = 260-64
= 196
|
|
Cf = 52+64
= 116
|
|
Cm = 0
|
|
C = 312
|
À ce prix-là, le fort ne peut consommer qu'une unité en plus, le faible 4 unités en moins. Il ne sera probablement pas d'accord de laisser (céder) l'outil en location à ce prix.
Remarquons que la situation de la mère a été négligée et reste à améliorer : le lecteur se fera une joie d'optimiser la ponction fiscale.
4. et si le petit bénéficiait d'un autre quota d'heures ?
Nous laissons au lecteur l'analyse d'une autre distribution de l'héritage, ou l'introduction de quota adaptée à la situation individuelle. La répartition du temps de travail serait la même, mais le malingre disposerait de d'avantage d'heures à mettre en location à son frère plus doué.
5. quid de Cornélius et son outil inutilisé ?
N'oublions pas Cornélius qui dispose d'un outil pour lui et sa fille. Son rôle sera d'attirer sur ses terres le costaud, en commençant par lui proposer un prix de location de l'outil plus faible, quitte à lui proposer à la fin, de devenir (co)propriétaire de l'outil. Le jeu de la concurrence se reconstruit et l'on pourrait imaginer qu'il aille travailler chez Cornélius, tout en louant l'outil à son frère.
V. Les notions abordées
|
La consommation
La consommation finale
La consommation productive
La production
La production moyenne
La production marginale
La raretédes moyens
Le travail et ses revenus
La propriétéet ses revenus
Le troc
|
L'offre
La demande
La monnaie
La formation des prix
Le rôle de l'État
Les retenues sociales et fiscales
La redistribution, la sécuritésociale, le minimex, les allocations
Le choix : moteur de l'économie
Le modèle économique
La location
|
|
♦ Une préparation type ?...Non !
(facture, note de débit, note de crédit)
|
INSTITUT NOTRE-DAME DE BONNE ESPÉRANCE
BRAINE-LE-COMTE
ÉCOLE NORMALE MOYENNE
|
1. L'ÉTUDIANT(E)
|
|
NOM et prénom : DUCELLIER Guy
Classe et section : 1ère régendat math sc.économiques
Nature du stage : stage d'essai
|
|
2. LEÇON
|
|
Maître de stage : Monsieur G.Meléco Branche : sciences éco
Type d'enseignement : technique de qualification Degré :
Option : secrétariat Classe : 4 Q S
Date(s) : du 22/4 au 5/5/99 Heure(s) : 3
Nombre d'élèves : 19 Local : 1023
|
|
Titre Factures, notes de débit, notes de crédit
Contenu Les éléments d'une facture
Les escomptes
Les remises, rabais, ristournes
Les emballages repris et non repris
Autres précisions
|
|
Prérequis
|
|
N°
|
prérequis
|
où
|
|
1
2
3
4
|
L'élève est capable de :
· reconnaître des éléments communs à plusieurs documents
· calculer un pourcentage
· calculer la T.V.A.
· arrondir les résultats
|
dans l'activité de découverte
dans les exercices
" "
" "
|
|
Objectifs en termes de compétences disciplinaires [1]
|
|
N°
|
compétences
|
où
|
|
1
2
3
4
5
6
|
L'élève sera capable de :
· retrouver les éléments essentiels d'une facture et les noter
· définir par écrit un escompte
· définir par écrit une remise
· définir par écrit un rabais
· définir par écrit une ristourne[2]
· remplir une facture sur base d'un énoncé
|
dans l'activité de découverte
au 3ème paragraphe
au 4ème " "
" "
" "
dans les exercices
|
|
Objectifs en termes de compétences transversales
|
|
N°
|
compétences
|
où
|
|
|
L'élève sera capable de :
· distinguer l'essentiel de l'accessoire
|
dans l'activité de découverte
|
Organisation du tableau
|
rabais
· réduction valeur
· qualiténon conforme
|
remise
· réduction valeur
· client fidèle / achat en quantité
|
ristourne
· réduction valeur
· tous les clients, mais période déterminée
|
puis, d'abord, au centre du T.N. ;
puis, ensuite, déplacé vers la gauche pour pouvoir faire les exercices à droite
|
S(q*P)
- RRR
sous total
- escompte
+ transport
+ emball n repr
base taxable
+ T V A
+ escompte
+ emball repris
À payer
|
Exercices
_ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _
|
puis exerc sur NdD/NdCr
|
. Q | libellé | PU | PT .
. | | | .
total :_ _ _ _ _ _
TVA :_ _ _ _ _ _
À payer :_ _ _ _ _ _
|
Plan de la leçon
Les factures
activité
correction activité
lecture des feuilles
exercices
Les notes de débit et notes de crédit
activité(= exercice sur la facture)
correction de l'activité
feuilles théorie
exercices
Les factures
A) Rappel
1) La facture
La facture est un document officiel, rédigé par le _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _, qui informe l'_ _ _ _ _ _ _ _ _ _ _ de la _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ à payer pour la commande qu'il a effectuée auprès du _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ [3]
2) Les éléments essentiels de la facture
· pour le vendeur,
· nom,
· adresse
· numéro de registre de commerce (R.C....)
· numéro de TVA[4]
· au moins un numéro de compte bancaire
· pour l'acheteur,
· nom,
· adresse
· ces deux derniers suivis du mot "DOIT (pour)"
· lieu et date de la rédaction de la facture
· numéro d'ordre de la facture[5]
· désignation des marchandises (quantité, références, prix unitaires...)
· base imposable de TVA (montant HTVA)
· taux et montant de TVA
· montant total à payer par l'acheteur
Ces éléments sont obligatoires, mais la présentation est laissée libre[6]
3) Les remises, ristournes, rabais et escompte
Il arrive couramment que la marchandise envoyée par un vendeur ne convienne pas tout à fait à l'acheteur. Ce dernier peut alors renvoyer la marchandise ou en négocier le prix.
A) Les rabais
a) définition
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ [7]
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
· Je dis "Je vais vous parler des factures"
· Je dis : "Vos avez déjà vu en partie cette matière l'an passé, on va donc revoir les notions que vous avez appris
· Je distribue feuille 1, feuille 2, et 2 documents
· En distribuant les feuilles, je dis : "Vous allez voir que sur ces feuilles, il y a 3 ou 4 définitions. Vous ne devez pas les connaître par cœur, simplement savoir les éléments importants. Pour moi, ce sont les lacunes du texte."
· Je demande à un élève : "Lis le premier paragraphe et essaie de compléter les lacunes"
· J'efface le tableau
· Je note les mots manquants au T.N.
· Je demande : "Notez au fur et à mesure les mots manquants"
· S'ils ne trouvent pas, je demande à un e : "Qui rédige la facture ?"
· Je demande à un e : "Lis le point 2"
· Je dem. "Quels sont les éléments importants dont tu te rappelles dans cette définition et que l'on pourrait mettre dans la définition de rabais ?"
· J'écris rabais du coté gauche du TN et je note les éléments que l'élève me dit en dessous
· Les éléments attendus sont "réduction de valeur"et la raison de cette réduction (= qualité non conforme)
· Si l'élève ne sait pas, je demande à un autre élève.
· "Fais une phrase correcte avec les éléments qui sont écrits au TN"
· Je corrige la phrase si nécessaire
· Je dem. "Répète pour que tous les autres puissent la copier"
|
[8]
[9]
[10]
[11]
[12]
[13]
|
10 min.
|
b) exemple
la diminution de prix accordée par un garagiste[14] sur la vente d'un véhicule pour une griffe occasionnée lors du transport du véhicule.
B) Les remises
a) définition
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
b) exemple
diminution de prix qu'un concessionnaire accorde à ses bons clients[15]
C)Les ristournes
a) définition
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
b) exemple
diminution de prix qu'un concessionnaire accorde pendant le salon de l'automobile
les soldes de juillet ou de janvier
Les remises, rabais et ristournes ne sont jamais soumis à la TVA.
Les sont rares sur une facture, car il faudrait que la facture soit rédigée après que l'acheteur ait examiné la marchandise reçue.
D) L'escompte conditionnel
a) définition
L'escompte conditionnel consiste en une _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _sur le prix, accordée en cas de _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
b) exemple
j'incite mon client à s'acquitter immédiatement de sa dette dans le délai fixé, s'il le fait[16], il pourra payer moins cher
Les escomptes ne sont jamais soumis à la TVA.
Les escomptes sont rarement déduits définitivement sur une facture, car il faudrait que la facture soit rédigée après que l'acheteur n'ait payé...d'où le fait de "rajouter"ce montant après le calcul de la TVA.
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
· même démarche pour remise et ristourne
· je note remise au milieu et ristourne à droite
· Les éléments attendus pour remise sont "réduction de valeur"et la raison de cette réduction (= achat régulier ou en quantité)
· Les éléments attendus pour ristourne sont "réduction de valeur", "accordée à tous les clients"et la raison de cette réduction (= moment dans l'année)
· pour l'escompte, je dem. : "Lis le paragraphe D"
· s'il ne trouve pas, je demande : "que fait l'escompte sur le total de la marchandise ?"
· "Oui, c'est bon ; mais on préfère dire "réduction de prix""
· "Quand cette réduction est-elle accordée ?"
· Je dis : "Un escompte c'est un cadeau que fait le vendeur pour être payé plus tôt. Si on a des problèmes de liquidités, cela peut être utile d'être payé rapidement."
|
"elle le diminue"[17]
[18]
"si on paie plus tôt"[19]
[20]
|
|
|
♦ Et cette préparation est-elle type ?
(indice et index)
|
INSTITUT NOTRE-DAME DE BONNE ESPÉRANCE
BRAINE-LE-COMTE
ÉCOLE NORMALE MOYENNE
|
1. L'ÉTUDIANT(E)
|
|
NOM et prénom : Depuydt Estelle
Classe et section : 3e régendat math sc.économiques
Nature du stage : stage dans l’enseignement général
|
|
2. LEÇON
|
|
Maître de stage : Monsieur Cauchie Branche : sciences éco
Type d'enseignement : général Degré : 2e degré
Option : sciences économiques et langues Classe : 3e Eco Langues
Date(s) : du 12/01 au 26/01/98 Heure(s) : 10
Nombre d'élèves : 23 Local : S 4
|
|
Titres L’indice, l’index
Contenu calcul + interprétation de l’indice
francs courants / francs constants
...
Autres précisions
|
|
Prérequis
|
|
N°
|
prérequis
|
où
|
|
1
2
3
4
|
L'élève est capable de :
· interpréter des données sous forme d’un texte
· construire un tableau, un graphique à partir de données sous forme d’un texte
· calculer un pourcentage (à l’aide de la règle de trois)
· arrondir les résultats
|
au point 1
au point 1
aux points 3 et 4
à chaque calcul
|
|
Objectifs en termes de compétences
|
|
N°
|
compétences
|
où
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
L'élève sera capable de :
· retirer des informations (telles que l’augmentation des prix, l’augmentation des quantités produites) d’un tableau, d’un graphique
· restituer la définition de l’indice
· préciser l’utilitéde l’indice
· calculer un indice (de volume et de prix) pour une année donnée à partir de prix donnés (ou quantités) et de la base donnée
· calculer des prix en fonction des indices donnés
· calculer l’augmentation (en valeur absolue et en valeur réelle) du prix d’un produit dont les prix sont donnés pour deux ou plusieurs années
· restituer la définition de l’index
· préciser le rôle de l’index
· définir francs courants, francs constants
· traduire en francs constants d’une année donnée des revenus exprimés en francs courants en utilisant l’index, et réciproquement
· représenter graphiquement l’évolution des revenus en francs constants et courants, et représenter graphiquement l’évolution du nombre de véhicules
· s’exprimer dans un langage clair et correct
· interpréter des nombres sous forme d’un texte
|
aux points 1, 4, 5 et 6
à la fin du point 3
à la fin du point 3
aux points 3, 4, 5 et 6
au point 4
aux points 4 et 5
questionnaire du texte : « L’index du coût de la vie en Belgique.
au point 6
au point 7
au point 7
à tout moment !
aux points 3, 4, 5, 6 et 7
|
Plan de la leçon
L’indice
1. Interpréter une évolution
interpréter des données sous forme d’un texte
construire un tableau
interpréter des données sous forme d’un tableau
construire un graphique
interpréter des données sous forme d’un graphique
2. Interpréter un indice
représenter graphiquement une évolution
interpréter
3. Calculer un indice
activité
correction activité
lecture des feuilles
exercices
Définition et utilité de l’indice
4. Calculer des prix et des quantités en fonction des indices donnés
activité
correction de l’activité
formule
5. Interpréter l’index
6. Distinguer un revenu nominal et un revenu réel
activité
correction activité
7. Traduire en francs constants d’une année donnée des revenus exprimés en francs courants
calcul
constatation
représentation graphique
Quelques tests
1. Interpréter une évolution
« Comment a évolué le nombre de voitures particulières en Belgique (depuis 1980) ?
En 1980, il y avait 3 159 000 voitures particulières. Dix ans plus tard, il y en avait 3 864 000. De 1990 à 1993, il y a eu une augmentation de 246 000 véhicules. En 1994, le nombre s’élevait à 4 210 000 et l’année suivante à 4 273 000 véhicules.
Interprète cette évolution.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Inscris ces résultats d’une autre manière.
Interprète cette évolution.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Inscris ces résultats d’une troisième manière.
Interprète cette évolution.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Constatations :
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
1. Interpréter une évolution
« Comment a évolué le nombre de voitures particulières en Belgique (depuis 1980) ?
En 1980, il y avait 3 159 000 voitures particulières. Dix ans plus tard, il y en avait 3 864 000. De 1990 à 1993, il y a eu une augmentation de 246 000 véhicules. En 1994, le nombre s’élevait à 4 210 000 et l’année suivante à 4 273 000 véhicules.
Interprète cette évolution.
Le nombre de voitures a augmenté de 1980 à 1995, il est passé de 3 159 000 à 4 273 000 véhicules .
Inscris ces résultats d’une autre manière.
|
Année
|
1980
|
1990
|
1993
|
1994
|
1995
|
|
Nombre de voitures
|
3 159 000
|
3 864 000
|
4 110 000
|
4 210 000
|
4 273 000
|
Interprète cette évolution.
L’augmentation a été plus forte durant les dix premières années (de 1980 à 1990) que pour les suivantes.
Inscris ces résultats d’une troisième manière.

Interprète cette évolution.
On peut, à présent, mieux voir l’augmentation du nombre de véhicules mais ce n’est pas encore très précis.
Constatations :
Ces différentes manières ne permettent pas d’interpréter cette évolution sous forme d’un pourcentage.
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
0. Introduction
· Jeudi dernier, ma petite sœur, en revenant de l’école, était très heureuse, elle avait eu 10/10 à sa dictée. Le lendemain, elle était un peu râleuse, alors je lui demande ce qu’il se passe et elle me répond qu’elle n’a eu que 5/10 à sa dictée.
Et le lundi, en revenant de l’école ça allait déjà mieux, elle me dit : "j’ai réussi à remonter de 50 % ". Quel sont ses points ?
· Les élèves vont sûrement me répondre 10/10, je leur répondrai que ce n’est pas faux mais qu’il faut tout simplement préciser par rapport à quelle note elle a augmentéde 50 %
· Nous venons de voir l’évolution des points de ma petite sœur, à présent nous allons essayer d’interpréter un autre type d’évolution
(Distribution de la page 1)
1. Interpréter une évolution
a) Activité(il s’agit d’interpréter des résultats sous différentes formes et de les organiser sous forme d’un tableau et d’un graphique qui sont tous deux construis par les élèves).
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
b) Correction de l’activité :
· Je demande à un élève de me donner l’interprétation qu’il a faite à partir du texte (en passant dans les bancs, j’ai vu qu’il avait répondu à la question).
· Y a-t-il d’autres manières de noter ces résultats ?
· Je demande à un élève de me donner l’interprétation qu’il a faite à partir du tableau.
· On peut encore noter ces résultats d’une troisième manière, laquelle ?
· Je demande à un élève de me donner l’interprétation qu’il a faite à partir du graphique.
c) Synthèse :
« Que peut-on constater à propos de ce que l’on vient de faire ?
|
Réponse attendue : 7,5 / 10
Les élèves lisent mentalement l’activité et la résolvent au crayon.
Temps accordéla réalisation de l’activité : 15 minutes.
Réponse attendue : on sait juste dire qu’il y a eu une augmentation du nombre de voitures entre 1980 et 1995.
Réponse attendue : sous forme d’un tableau
Un élève vient construire ce tableau au TN.
Réponse attendue : les élèves peuvent donner plus facilement l’évolution en nombre de voitures mais cette interprétation ne me dit rien.
Réponse attendue : sous forme d’un graphique.
Un élève vient construire ce graphique au TN.
Réponse attendue : on voit mieux l’évolution en comparant les différentes hauteurs des bâtons, mais ce n’est pas très précis.
Réponse attendue : on ne peut pas voir très clairement l’évolution réelle du nombre de voitures à partir de ces différentes manières (on ne peut quantifier cette augmentation.
|
5 min
15 min
10 min
5 min
|
2. Interpréter un indice
« Que sont devenus mes 100 de départ ?
$$$$
(Source : La Libre Belgique. Octobre 1996)
Représente graphiquement l’évolution du nombre de voitures particulière en faisant attention aux différents « écarts qu’il y a entre les dates.
3. Calculer un indice
Afin d’interpréter à l’aide d’un pourcentage cette évolution, nous allons nous faciliter la tâche en donnant au nombre de départ (1980) la valeur 100.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Que valent les indices des autres années (sur base 100 en 1980) ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
2. Interpréter un indice
« Que sont devenus mes 100 de départ ?
(Source : La Libre Belgique. Octobre 1996)
Représente graphiquement l’évolution du nombre de voitures particulière en faisant attention aux différents « écarts qu’il y a entre les dates.

3. Calculer un indice
Afin d’interpréter à l’aide d’un pourcentage cette évolution, nous allons nous faciliter la tâche en donnant au nombre de départ (1980) la valeur 100.
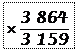



 (1980) 3 159 100
(1980) 3 159 100

 (1990) 3 864 122,32
(1990) 3 864 122,32
En 10 ans, de 1980 à 1990, le nombre de voitures a augmentéde 22,3 %
Que valent les indices des autres années (sur base 100 en 1980) ?
(1993) 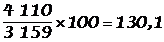 .
.
De 1980 à 1993, le nombre de voitures a augmentéde 30,1 %.
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Distribution de la page 2)
2. Interpréter un indice
· Que constatez-vous en comparant le graphique de la page 2 avec celui que vous avez construis ?
a) Activité(il s’agit de représenter graphiquement l’évolution de la manière la plus correcte c’est-à-dire en faisant attention à la ligne du temps).
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
b) Correction de l’activité :
· Je demande à un élève de venir faire le graphique au tableau
c) Interprétation :
· Je demande à un élève de me donner l’interprétation qu’il a faite à partir de ce graphique.
3. Calculer un indice
a) Méthode de calcul.
· Je résous l’exercice avec l’aide des élèves au TN (règle de 3), les autres élèves écoutent attentivement et à la fin de la résolution, ils peuvent poser des questions si quelque chose n’est pas compris.
· J’introduis le mot « indice en disant que c’est le nombre que l’on obtient (je le montre).
b) Activité (il s’agit de calculer des indices).
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
c) Correction de l’activité :
· Je demande à une élève de venir expliquer la méthode de calcul
|
Réponse attendue : sur le graphique de la page 2, il manque une partie des bâtonnets (de 0 à 3000), on a l’impression qu’il y a eu une très forte augmentation entre 1980 et 1995.
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
Temps accordéla réalisation de l’activité : 5 minutes.
Un élève vient construire le graphique au TN
Réponse attendue : il y a eu une faible augmentation entre 1980 et 1995.
Un élève lit oralement l’énoncé.
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
Temps accordéla réalisation de l’activité : 10 minutes.
Un élève vient expliquer la méthode de calcul, les autres l’écoutent (idem pour le deuxième).
|
5 min
5 min
5 min
5 min
10 min
10 min
|
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Interprète à l’aide d’un pourcentage l’évolution qu’il y a eu entre 1994 et 1995 ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
 Lorsqu’on interprète une évolution, il faut toujours bien préciser par rapport à quelle année on se réfère.
Lorsqu’on interprète une évolution, il faut toujours bien préciser par rapport à quelle année on se réfère.
Écris une formule qui te permet de calculer un indice pour une année donnée :
Évolution de la population (en milliers)
(Source : La Libre Belgique. Octobre 1996)
1. Que signifie l’indice de 1995 pour la population féminine en prenant comme année de référence 1990 ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
(1994) 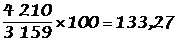 .De 1980 à 1994, augmentation de 33,3 %.
.De 1980 à 1994, augmentation de 33,3 %.
(1995) 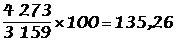 .De 1980 à 1995, augmentation de 35,3 %.
.De 1980 à 1995, augmentation de 35,3 %.
Interprète à l’aide d’un pourcentage l’évolution qu’il y a eu entre 1994 et 1995 ?
Si j’interprète l’évolution qu’il y a eu entre 1994 et 1995, il faut que je prenne 1994 comme année de référence.
(1995) 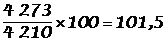 .De 1994 à 1995, augmentation de 1,5 %.
.De 1994 à 1995, augmentation de 1,5 %.
Sur base de l’année 1980, il y a eu une augmentation de 1,99 % (133,27-135,26)
 Lorsqu’on interprète une évolution, il faut toujours bien préciser par rapport à quelle année on se réfère.
Lorsqu’on interprète une évolution, il faut toujours bien préciser par rapport à quelle année on se réfère.
Écris une formule qui te permet de calculer un indice pour une année donnée :

Évolution de la population (en milliers)
(Source : La Libre Belgique. Octobre 1996)
1. Que signifie l’indice de 1995 pour la population féminine en prenant comme année de référence 1990 ?
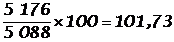 . L’indice 101,73 de 1995 (base 100 en 1990) signifie que la population féminine a augmenté de 1,73 % entre 1990 et 1995.
. L’indice 101,73 de 1995 (base 100 en 1990) signifie que la population féminine a augmenté de 1,73 % entre 1990 et 1995.
|
Activité du maître
|
Activité de l'élève
|
Timing
|
|
(Distribution de la page 3)
d) Interpréter un indice
· Comment interpréter l’évolution du nombre de voiture entre 1994 et 1995 ?
· Je demande à un élève de me donner l’interprétation qu’il a faite à partir des indices.
! Préciser par rapport à quelle année on se réfère (voir introduction)
e) Activité(formule)
Àpartir des trois indices qui viennent d’être calculé, les élèves essayent de trouver une formule qui permet de calculer un indice pour une année donnée.
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
f) Correction de l’activité :
Un élève vient noter la formule qui permet de calculer un indice, les autres l’écoutent
g) Exercices (évolution de la population)
· Exercice 1
Je demande aux élèves de regarder le graphique et d’en donner l’allure générale.
Je demande à un élève de me donner l’interprétation qu’il a faite à partir de l’indice de 1995 sur base de 1990 pour la population féminine.
· Correction de l’exercice 1
Je demande à un élève de venir calculer l’indice de 1995 et d’expliquer comment il procède.
« Que signifie l’indice de 1995 pour la population féminine en prenant comme année de référence 1990 ?
|
Réponse attendue : à l’aide des indices
Réponse attendue : il y a eu une augmentation du nombre de voitures de 1,5 % (si l’on se base sur 1994).
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
* entourer ce qui a de commun à chaque calcul
* nommer ces parties communes
Temps accordéla réalisation de l’activité : 5 minutes.
Réponse attendue : voir feuille élève page 3.
Temps accordéla réalisation des exercices : 20 minutes.
Les élèves regardent le graphique.
Réponse attendue : De 1980 à 1995, les populations féminines et masculines ont évoluépeu près de la même manière. Elles sont en augmentation.
Les élèves doivent tout d’abord calculer l’indice de 1995 et ensuite, l’interpréter. (Ils font tout ça au crayon)
Réponse attendue : 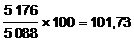 . .
Réponse attendue : De 1990 à 1995, la population féminine a augmentéde 1,73 % (sur base de 1990).
|
10 min
5 min
5 min
5 min
5 min
5 min
5 min
|
2. Que signifie l’indice de 1995 pour la population masculine en prenant comme année de référence 1980 ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
3. Réponds par vrai ou par faux en justifiant ta réponse.
L’interprétation du graphique nous indique que :
a) en 5 ans, de 1990 à 1995, la population féminine a augmentéde 3 %
c’est ............... car _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
b) en 10 ans, de 1980 à 1990, la population masculine a augmentéde 3 %
c’est ............... car _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
c) de 1994 à 1995, les populations féminine et masculine ont augmentéde la même manière
c’est ............... car _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

2. Que signifie l’indice de 1995 pour la population masculine en prenant comme année de référence 1980 ?
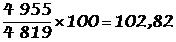 . L’indice 102,82 de 1995 (base 100 en 1980) signifie que la population masculine a augmentéde 2, 82 % entre 1980 et 1995.
. L’indice 102,82 de 1995 (base 100 en 1980) signifie que la population masculine a augmentéde 2, 82 % entre 1980 et 1995.
3. Réponds par vrai ou par faux en justifiant ta réponse.
L’interprétation du graphique nous indique que :
a) en 5 ans, de 1990 à 1995, la population féminine a augmentéde 3 %
c’est faux car elle a augmentéde 1,73 %.
b) en 10 ans, de 1980 à 1990, la population masculine a augmentéde 3 %
c’est vrai car (102,82) si on arrondit à l’unitésupérieure, mais si on veut être précis, c’est une augmentation de 2,82 %.
c) de 1994 à 1995, les populations féminine et masculine ont augmentéde la même manière
c’est faux car il y a une augmentation de 0,31 % de la population féminine et une augmentation de 0,30 % de la population masculine (à 0,01 % près !)

|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Distribution de la page 4)
· Exercice 2
Je demande à un élève de me donner l’interprétation qu’il a faite à partir de l’indice de 1995 sur base de 1980 pour la population masculine.
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
· Correction de l’exercice 2
Je demande à un élève de venir calculer l’indice de 1995 et d’expliquer comment il procède.
« Que signifie l’indice de 1995 pour la population masculine en prenant comme année de référence 1980 ?
· Exercice 3
Il s’agit de répondre par vrai ou faux à 3 affirmations et ensuite de justifier chaque réponse.
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
· Correction de l’exercice 3
Pour chaque affirmation, je demande à un élève de me dire si elle est vrai ou fausse et de justifier sa réponse en interprétant.
h) Synthèse (à partir de la formule qui permet de calculer l’indice) :
· Comment pourrait-on définir un indice ?
· Comment trouve-t-on ce nombre ?
· « Quelle est l’utilitéde l’indice ?
|
Les élèves regardent le graphique.
Les élèves doivent tout d’abord calculer l’indice de 1995 et ensuite, l’interpréter. (Ils font tout ça au crayon)
Réponse attendue : 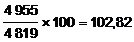 . .
Réponse attendue : De 1980 à 1995, la population masculine a augmentéde 2,82 % (sur base de 1980).
Les élèves lisent mentalement l’exercice 3 et le résolvent au crayon.
Temps accordéla réalisation de l’activité : 10 minutes.
Réponse attendue : voir feuille-élève page 4.
Réponse attendue : c’est un nombre.
Réponse attendue : on fait le rapport entre un nombre (ou la grandeur d’un élément) à un moment donnéet ce même nombre à une période de référence et on multiplie ce rapport par 100.
Réponse attendue : l’indice permet d’analyser facilement une évolution.
|
10 min
5 min
5 min
15 min
5 min
5 min
|
4. Calculer des prix et des quantités en fonction des indices donnés
Tableau représentant l’évolution des quantités produites (indice de volume) et des prix du chocolat (indice de prix).
|
|
1950
|
1960
|
1970
|
1980
|
1991
|
1997
|
|
indice de volume
|
100
|
121
|
142
|
289
|
347
|
301
|
|
indice de prix
|
100
|
112
|
145
|
315
|
436
|
533
|
Supposons qu’en moyenne une personne consommait 250 g de chocolat, par mois, en 1950.
Quelle est la quantitémoyenne de chocolat en 1980 ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Inscris la formule à utiliser :
Si 1 kilo de chocolat coûte 295 EUR en 1997, quel est son prix en :
1950 ? _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
1980 ? _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Inscris la formule à utiliser :
4. Calculer des prix et des quantités en fonction des indices donnés
Tableau représentant l’évolution des quantités produites (indice de volume) et des prix du chocolat (indice de prix).
|
|
1950
|
1960
|
1970
|
1980
|
1991
|
1997
|
|
indice de volume
|
100
|
121
|
142
|
289
|
347
|
301
|
|
indice de prix
|
100
|
112
|
145
|
315
|
436
|
533
|
Supposons qu’en moyenne une personne consommait 250 g de chocolat, par mois, en 1950.
Quelle est la quantitémoyenne de chocolat consommée en 1980 ?
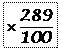
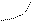


 (1950) 100 250
(1950) 100 250

 (1980) 289 722,5
(1980) 289 722,5
En 1980, on consommait en moyenne 722,5 g de chocolat.
Inscris la formule à utiliser :
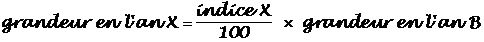
Si 1 kilo de chocolat coûte 295 BEF en 1997, quel est son prix en :
1950 ? 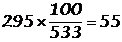
1980 ? 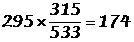
Inscris la formule à utiliser :
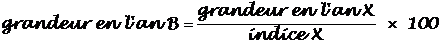
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Distribution de la page 5)
4. Calculer des prix et des quantités en fonction des indices donnés
a) Activité(voir titre)
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
b) Correction de l’activité :
· À votre avis, qu’est-ce qu’un indice de volume ?
· Que représentent les indices de prix ?
· Que doit-on rechercher ?
· P envoie un élève au TN pour noter et expliquer la méthode de résolution (par une règle de 3).
· Que doit-on rechercher ?
· P envoie un élève au TN pour noter et expliquer la méthode de résolution (par une règle de 3).
|
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
Temps accordéla réalisation de l’exercice : 15 minutes.
Réponse attendue : c’est un nombre représentant l’évolution des quantités produites.
Réponse attendue : l’évolution des prix du chocolat
Réponse attendue : la quantitémoyenne de chocolat consommée en 1980.
Les élèves doivent inscrire une formule, sur base de l’exercice, pour retrouver les quantités.
Réponse attendue : le prix du chocolat en 1960 et en 1980.
Les élèves doivent inscrire une formule, sur base de l’exercice, pour retrouver les prix
|
15 min
5 min
5 min
10 min
|
5. Interpréter l’index
Évolution de certains prix (en BEF)
|
|
1970
|
1997
|
|
un litre de lait
une place de cinéma
un exemplaire du journal « Le Soir
un pain
un paquet de cigarettes
une consultation médicale (généraliste)
|
7
40
4
13
10
102
|
30
220
28
57
125
580
|
Calcule l’indice de variation des prix pour deux produits (au choix).
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Compare les deux évolutions.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
6. Distinguer un revenu nominal et un revenu réel
Évolution des revenus (brut) d’un employéde 1970 à 1997
|
Année
|
1970
|
1980
|
1997
|
|
Revenu
|
15 140 BEF
|
47 850 BEF
|
78 525 BEF
|
|
Indice
|
|
|
|
Que peut-on déduire de la comparaison de ces trois nombres ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Dans ce cas-ci les revenus sont exprimés en valeur _ _ _ _ _ _ c’est-à-dire en francs _ _ _ _ _ _ _
Peut-on pour autant en conclure que le pouvoir d’achat de l’employéa évoluédans le même sens et dans la même proportion entre 1970 et 1997 ?
5. Interpréter l’index
Evolution de certains prix (en BEF)
|
|
1970
|
1997
|
|
un litre de lait
une place de cinéma
un exemplaire du journal « Le Soir
un pain
un paquet de cigarettes
une consultation médicale (généraliste)
|
7
40
4
13
10
102
|
30
220
28
57
125
580
|
Calcule l’indice de variation des prix pour deux produits (au choix).
(lait) 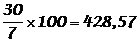 . Entre 1970 et 1997, le prix du lait a augmentéde 329 %.
. Entre 1970 et 1997, le prix du lait a augmentéde 329 %.
(pain) 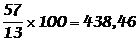 . Entre 70 et 97, le prix du pain a augmentéde 338 %.
. Entre 70 et 97, le prix du pain a augmentéde 338 %.
Compare les deux évolutions.
Les prix du pain et du lait ont à peu près évoluéde la même manière.
6. Distinguer un revenu nominal et un revenu réel
Évolution des revenus (brut) d’un employé de 1970 à 1997
|
Année
|
1970
|
1980
|
1997
|
|
Revenu
|
15 140 BEF
|
47 850 BEF
|
78 525 BEF
|
|
Indice
|
100
|
316
|
519
|
Que peut-on déduire de la comparaison de ces trois nombres ?
Entre 1970 et 1980, les revenus ont triplé et entre 1970 et 1997, ils ont été multipliés par 5.
Dans ce cas-ci les revenus sont exprimés en valeur nominale c’est-à-dire en francs courants.
Peut-on pour autant en conclure que le pouvoir d’achat de l’employé a évolué dans le même sens et dans la même proportion entre 1970 et 1997 ?
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Les élèves reçoivent le texte : L’index du coût de la vie en Belgique et un questionnaire qui est à faire en devoir à la maison)
(Distribution de la page 6)
5. Interpréter l’index
· Qu’est-ce qu’un index ?
a) Activité(calculer et interpréter l’index)
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
b) Correction de l’activité :
· P a préparésur un transparent les évolutions de prix de chaque produit de manière à ce que tous les élèves retrouvent l’indice des 2 produits choisis.
· P demande à un élève de comparer l’évolution des 2 produits qu’il a choisi (ex : le lait et le pain).
6. Distinguer un revenu nominal et un revenu réel
a) Activité(évolution des revenus d’un employéentre 1970 et 1997)
· Je demande aux élèves de regarder les trois revenus et d’essayer de quantifier l’évolution sans calculer les indices
· Ensuite, je leur demande de calculer les indices pour chaque année en prenant comme année de référence 1970.
· Et enfin, je leur demande de comparer ces trois nombres.
b) Correction de l’activité
au TN
c) Pouvoir d’achat
· Qu‘est-ce que le pouvoir d’achat ?
· Peut-on dire que l’employéa pu se procurer 3 fois plus de biens en 1980 qu’en
1970 ?
|
Réponse attendue : Un index est un indice particulier. C’est l’indice des prix à la consommation.
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
Temps accordéla réalisation de l’exercice : 10 minutes.
Réponse attendue : Entre 1970 et 1997, les prix du pain et du lait ont à peu près évoluéde la même manière.
Les élèves résolvent l’activitéau crayon.
Temps accordéla réalisation de cette activité : 5 minutes.
Un élève vient noter les trois indices et explique comment il a procédé.
Ensuite, un autre élève dit oralement la comparaison des trois nombres. (voir feuille-élève page 6)
Réponse attendue : c’est la quantitéde biens et de services que l’on peut se procurer à l’aide de son revenu disponible.
Réponse attendue : on ne sait pas répondre précisément à cette question mais j’imagine que c’est non !
|
5 min
10 min
5 min
5 min
10 min
5 min
5 min
|
Pour répondre à cette question, nous avons besoin de connaître la manière dont les prix ont évolué entre ces époques.
Évolution de l’index de 1970 à 1998 (base 1966 = 100)
|
Années
|
1970
|
1980
|
1998
|
|
Index
|
113,94
|
231,87
|
424,90
|
Que peut-on constater ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Il faut dès lors considérer le revenu disponible en valeur ................ c’est-à-dire en francs _ _ _ _ _ _
7. Traduire en francs constants d’une année donnée des revenus exprimés en francs courants
Calcule ce que représente les revenus de 1970, 1980 et 1998 en francs de 1998.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Il nous est maintenant possible de dresser un tableau beaucoup plus significatif de l’évolution réelle du revenu disponible d’un employé.
Complète le tableau ci-dessous :
|
Années
|
Revenus en francs courants
|
Indice de croissance
|
Index
|
Revenus en BEF de 1998.
|
Indice de croissance
|
|
1970
1980
1998
|
_ _ _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
|
..................
..................
..................
|
..........
..........
..........
|
_ _ _ _ _ _
_ _ _ _ _ _
_ _ _ _ _ _
|
..................
..................
...................
|
Pour répondre à cette question, nous avons besoin de connaître la manière dont les prix ont évolué entre ces époques.
Evolution de l’index de 1970 à 1998 (base 1966 = 100)
|
Années
|
1970
|
1980
|
1997
|
|
Index
|
113,94
|
231,87
|
424,90
|
Que peut-on constater ?
Les prix ont doubléentre 1970 et 1980 et ont quadruplé entre 70 et 97.
Il faut dès lors considérer le revenu disponible en valeur réelle c’est-à-dire en francs constants.
7. Traduire en francs constants d’une année donnée des revenus exprimés en francs courants
Calcule ce que représente les revenus de 1970, 1980 et 1997 en francs de 1970.
(1980) 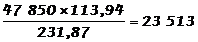 . Le revenu de l’employé en 1980 représente 23 513 BEF de 1970.
. Le revenu de l’employé en 1980 représente 23 513 BEF de 1970.
(1997) 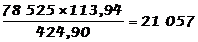 . Le revenu de l’employé en 1997 représente 21 057 BEF de 1970.
. Le revenu de l’employé en 1997 représente 21 057 BEF de 1970.
Il nous est maintenant possible de dresser un tableau beaucoup plus significatif de l’évolution réelle du revenu disponible d’un employé.
Complète le tableau ci-dessous :
|
Années
|
Revenus en francs courants
|
Indice de croissance
|
Index
|
Revenus en BEF de 1970.
|
Indice de croissance
|
|
1970
1980
1997
|
15 140 BEF
47 850 BEF
78 525 BEF
|
100
316
519
|
113,94
231,87
424,90
|
15 140 BEF
23 513 BEF
21 057 BEF
|
100
155
139
|
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Distribution de la page 7)
· Je demande aux élèves de regarder le tableau avec les index
· Que peut-on constater ?
· On ne peut pas comparer des francs de 1970 avec des francs de 1997.
« Pourquoi ?
Pour pouvoir comparer ces trois revenus, nous allons les mettre tous sur la « même base c’est-à-dire que l’on va les traduire en francs d’une même année.
7. Traduire en francs constants d’une année donnédes revenus exprimés en francs courants
a) Activité1(voir titre)
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
b) Correction de l’activité 1:
· Le premier exercice (pour l’année 1980) est fait avec l’ensemble de la classe.
· P demande à un élève de venir expliquer comment on procède pour le deuxième exercice (pour l’année 1997).
c) Activité2 (tableau)
· Je demande aux élèves de compléter le tableau pour pouvoir voir l’évolution réelle du revenu de l’employé.
d) Correction de l’activité2
· Sur transparent, on complète le tableau en expliquant comment on a procédépour trouver chaque nombre.
|
Réponse attendue : On constate que les prix ont doubléde 1970 à 1980 et ils ont quadrupléentre 1970 et 1997.
Réponse attendue : un billet de 1000 BEF en 1970 n’a pas la même valeur qu’un billet de 1000 BEF en 1997. En effet, en 1970, avec 1000 BEF je peux acheter 25 places de cinéma. Tandis qu’en 1997, je ne peux en acheter que 5.
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
Temps accordéla réalisation de l’exercice : 10 minutes.
Réponse attendue : pour traduire le revenu de 1997 en francs de 1970, on multiplie ce revenu par l’index de l’année de base (1970) et on divise par l’index de 1997.
Les élèves résolvent l’activité2 au crayon.
Temps accordéla réalisation de cette activité : 5 minutes.
|
5 min
10 min
10 min
5 min
5 min
10 min
|
Constatations :
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Représente graphiquement l’évolution - en francs courants (en vert)
- en francs constants (en rouge)
du revenu disponible de l’employé entre 1970 et 1997..
Constatations :
En francs constants de 1970, on constate que le revenu de l’employé a augmenté de 55 % entre 70 et 80 et a diminué de 16 % entre 70 et 97 (sur base de 1970)
Représente graphiquement l’évolution - en francs courants (en vert)
- en francs constants (en rouge)
du revenu disponible de l’employéentre 1970 et 1997.

|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Distribution de la page 8)
· A partir de ce tableau quels sont vos constatations ?
d) Activité3 (représenter graphiquement l’évolution du revenu de l’employé)
Pendant ce temps, je passe dans les bancs afin de voir les réponses des élèves (je ne dis rien).
e) Correction de l’activité3 :
· P a demande à un élève de venir tracer les axes (avec la bonne échelle)
· Un autre élève vient tracer l’évolution du revenu de l’employéen francs courants
· Un autre élève vient tracer l’évolution du revenu de l’employéen francs constants
|
Les élèves lisent mentalement l’activité3 et la résolvent au crayon.
Temps accordéla réalisation de l’exercice : 10 minutes.
Réponses attendues : voir feuille-élève page 8
|
10 min
15 min
|
8. Calculer un index
Voici l’extrait d’un contrat de bail :

Le 15 octobre 1988, mon loyer s’élevait à _ _ _ _ _ BEF.
En te référant à l’index de décembre 1997, calcule le montant du loyer pour janvier 1998.
|
L'index de décembre (LLB 27/12/97)
|
|
indice santé
Base 1988
Base 1981
Base 1974-75
Base 1971
Base 1966
|
122,68
125,21
169,38
260,86
357,39
424,90
|
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
8. Calculer un index
Voici l’extrait d’un contrat de bail :

Le 15 octobre 1988, mon loyer s’élevait à 18 000 BEF.
En te référant à l’index de décembre 1997, calcule le montant du loyer pour janvier 1998.
|
L'index de décembre (LLB 27/12/97)
|
|
indice santé
Base 1988
Base 1981
Base 1974-75
Base 1971
Base 1966
|
122,68
125,21
169,38
260,86
357,39
424,90
|
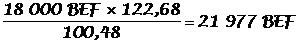
|
Activitédu maître
|
Activitéde l'élève
|
Timing
|
|
(Distribution de la page 9)
8. Calculer un index
· Lorsqu’on loue un appartement ou une maison, on doit signer un contrat de bail avec le propriétaire.
Tous les mois, il faudra payer un loyer. Ce loyer est indexé.
· Que veut dire un loyer indexé ?
a) Activité(calculer un loyer à l’aide de l’index)
b) Correction de l’activité :
· Àcombien s’élève le loyer en 1988 ?
· Quel sera le montant du loyer en 1997 ?
|
Réponse attendue : ça veut dire que le loyer suit l’évolution des prix. Donc si les prix augmentent, alors le prix du loyer va augmenter. (Idem pour une diminution des prix).
Les élèves lisent mentalement l’activitéet la résolvent au crayon.
Temps accordéla réalisation de l’exercice : 10 minutes.
Réponse attendue : 17 280 BEF + 720 BEF = 18 000 BEF.
Réponse attendue : 21 977 BEF (voir feuille-élève 9)
|
10 min
10 min
10 min
|
L’index du coût de la vie en Belgique
La composition du panier
L’indice des prix à la consommation est basé sur un panier de produits et services dont la composition est déterminée à l’issue d’une enquête sur les budgets des ménages. Réalisée par l’Institut national de statistique (INS), cette enquête vise à savoir comment les habitants du royaume répartissent leur revenu disponible et, dans la part réservée à la consommation, quelle pondération il faut attribuer à chacune des grandes catégories de dépenses. La dernière grande enquête de l’INS a été réalisée en 1987-1988 auprès de 3.315 ménages représentatifs de l’ensemble des catégories socio-professionnelles du pays (composition, revenu, etc.).
Les relevés des prix
Les prix sont relevés, dans leur grande majorité, directement dans plusieurs milliers de points de vente et on ne prend en considération que les prix effectifs, y compris les réductions.
Toutes les formes de distribution sont concernées, de l’hypermarché au petit commerce indépendant en passant par les coopératives et les sociétés de vente par correspondance. Et chacune de ces catégories est retenue en fonction de la part qu’elle occupe dans les habitudes de consommation des ménages. Pour quelques services, comme la redevance radio télévision, le prix de la SNCB ou la RTT - Belgacom, les assurances, les relevés sont effectués sur la base des tarifs pratiqués.
Une deuxième pondération est opérée sur le plan géographique cette fois. Les relevés sont effectués dans 65 localités réparties dans les 9 provinces (32 en Flandres, 32 en Wallonie et une à Bruxelles). Cet échantillon est censé représenter l’ensemble de la population belge et sa répartition dans tout le pays.
Dispositifs antidérapages
Le meilleur garde-fou contre une manipulation tendancieuse est la Commission de l’indice, composée de 7 professeurs d’université et de 14 représentants des interlocuteurs sociaux. Elle a pour mission d’examiner les relevés mensuels et aussi de se prononcer sur tous les problèmes qui surgissent à propos de l’indice.
Certes, elle ne dispose guère que d’une compétence d’avis, mais elle est généralement suivie par le décideur final, à savoir le ministre des Affaires économiques.
Éco-Soir, 31/12/93
Nom : _ _ _ _ _ _ _ _ Le .... ................ 199..
L’index du coût de la vie en Belgique
1. Recherche la signification de ces différents termes (en fonction du contexte) :
pondération : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
prix effectifs : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
coopérative :_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
interlocuteur social : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
2. Que détermine l’enquête sur les budgets des ménages ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
3. Qu’est-ce que l’index ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
4. Quel est son rôle ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
5. En quoi consistent les relevés mensuels ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
6. Quel est le rôle de la Commission de l’indice ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Nom : _ _ _ _ _ _ _ _ Le 29 janvier 1998.
Prénom : _ _ _ _ _ _ _
Classe : _ _ _ _ _ _ _
L’indice : test
$$$$
Fiche de l’actualité. Le Soir du 07.05.95
1. Interprète à l’aide d’un pourcentage l’évolution du nombre de salles de cinéma qu’il y a eu entre 1980 et 1993.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
2. Complète ce tableau (à partir du graphique) :
|
|
1960
|
1970
|
1980
|
1990
|
1997
|
|
Tickets vendus
|
|
|
|
|
|
|
Indices
|
|
|
|
|
45
|
|
Indices de prix
|
100
|
210
|
328
|
450
|
548
|
3. Si une place de cinéma coûte 150 BEF en 1990, quel est son prix en 1960 ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
4. Combien de tickets ont étévendus en 1997 ?
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Nom : _ _ _ _ _ _ _ _ Le 27 janvier 1998.
Prénom : _ _ _ _ _ _ _
Classe : _ _ _ _ _ _ _
L’indice : test 2
Réponds par vrai ou faux en entourant la bonne réponse. Pour chaque affirmation, justifie en écrivant le calcul qui te permet d’obtenir la bonne réponse (au verso de cette feuille).
Pour les affirmations 1, 2 et 3, on considère le graphique ci-dessous :
1. Entre 1970 et 1980, il y a eu une diminution de 29 % du nombre de spectateurs sur base de 1970. VRAI FAUX
2. Entre 1992 et 1996, il y a eu une augmentation de 6 % du nombre de spectateurs sur base de 1960. VRAI FAUX
3. En supposant que l’indice de 1997 est 35 (base 1960 = 100), il y a eu 29 825 000 spectateurs en Belgique en 1997. VRAI FAUX
Pour l’affirmation 4, on considère le tableau ci-dessous donnant l’évolution des prix des places de cinéma.
|
|
1960
|
1970
|
1980
|
1990
|
1997
|
|
Indices de prix
|
100
|
201
|
312
|
499
|
550
|
4. Une place de cinéma coûtait 120 BEF en 1980 (220 BEF en 1997).
VRAI FAUX
NOM : Le 10 février 1998.
Prénom : _ _ _ _ _
Classe : _ _ _ _ _ _
L’indice : test de synthèse
Voici un tableau représentant le nombre de personnes qui ont participé à certains Jeux Olympiques :
|
|
Athènes 1896
|
Londres 1908
|
Berlin 1936
|
Atlanta 1996
|
|
Homme
|
245
|
2035
|
|
6500
|
|
Femme
|
0
|
36
|
328
|
3700
|
1. Interprète à l’aide d’un pourcentage l’évolution du nombre de participantes qu’il y a eu entre 1908 et 1996. (3 points)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
2. En supposant que l’indice de 1936 est 193,4 (base 1908 = 100), combien y a-t-il eu de participants (hommes) en 1936 ? (3 points)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Voici un tableau représentant le coût de la vie en BEF :
|
|
1953
|
1963
|
1973
|
1983
|
1993
|
|
1 kg d’entrecôte (prix)
|
103 BEF
|
128 BEF
|
271 BEF
|
487 BEF
|
542 BEF
|
|
1 vol Bruxelles - New York
|
27 900 BEF
|
27 075 BEF
|
|
21 740 BEF
|
19 945 BEF
|
|
Indices de prix (Avion)
|
100
|
97,04
|
44, 87
|
77, 92
|
71,48
|
|
Index
|
100
|
210
|
328
|
450
|
548
|
3. Combien coûte un ticket d’avion Bruxelles - New York en 1973 ? (2 points)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
4. Exprime en francs de 1953 le prix d’1 kg d’entrecôte en 1963, 1673, 1983 et en 1993. (4 points)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
5. Représente graphiquement l’évolution en francs courants et en francs constants d’1 kg d’entrecôte entre 1953 et 1993. (8 points)
|
|
|
|
|
|
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
|
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
|
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
|
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _
|
|
♦ Algèbre financière : un sujet économique parmi d'autres...
|
-
Intérêts simples
-
Intérêts composés
-
Annuités
-
Emprunts
-
En résumé
-
Exercices
I. Intérêts simples
-
exemple introductif
-
démonstration ou monstration
-
exemple chiffré et remarque
Quelle est la valeur acquise par 8500 €, placés sur un carnet d'épargne pendant 6 ans à 4,5 % (on retire les intérêts chaque année).. // Confusion intérêt (i) et taux d'intérêt (r)
A. Exemple introductif
|
CAPITAL
|
INTÉRÊT
|
|
Je place 10000 € pendant 10 ans...à 10 %
mon capital devient :
an 0 : 10000
an 1 : 10000 + 1000 = 11000
an 2 : 11000 + 1000 = 12000
an 3 : 12000 + 1000 = 13000
an 4 : 13000 + 1000 = 14000
etc...
|
Je place 10000 € pendant 10 ans...à 10 %
mon intérêt devient :
an 0 : 0
an 1 : 1000
an 2 : 2000
an 3 : 3000
an 4 : 4000
etc...
|
L’intérêt : c’est la somme que rapporte un capital placé, c'est le prix de la privation de l'utilisation de ce capital.
Taux d’intérêt : c’est un pourcentage qui détermine le revenu annuel d’un capital placé.
Le capital de départ : c’est une somme d’argent possédée par un individu, une famille ou une entreprise et pouvant rapporter un intérêt.
Formule du calcul de l'intérêt :
B. Démonstration ou monstration ?
|
CAPITAL
|
INTÉRÊT
|
|
C0 = capital de départ
Ci = capital à la ie période
Cn = capital à la ne période
r = taux d'intérêt (rate)
n = durée du placement en période
* première année
C1 = capital + intérêt
= C0 + C0 * r
= C0 * ( 1 + r )
* deuxième année
C2 = capital + intérêt
= C0 * ( 1 + r ) + C0 * r
= C0 * ( 1 + r + r )
= C0 * ( 1 + 2 * r )
* ne année
Cn = capital + intérêt
= Cn-1 + C0 * r
= C0 * ( 1 + (n-1) * r ) + C0 * r
= C0 * [ 1 + (n-1) * r ) + r ]
= C0 * ( 1 + n * r )
|
C0 = capital de départ
Ii = intérêt de la ie période
In = intérêt de la ne période
r = taux d'intérêt (rate)
n = durée du placement en période
* première année
I1 = intérêt
= C0 * r
=
* deuxième année
I2 = I1 + intérêt
= C0 * r + C0 * r
= C0 * ( r + r )
= C0 * ( 2 * r )
* ne année
In = In-1 + intérêt
= In-1 + C0 * r
= C0 * ( (n-1) * r ) + C0 * r
= C0 * [ (n-1) * r ) + r ]
= C0 * n * r
|
C. Exemple chiffré et remarque
1. Quelle est la valeur acquise par 8500 €, placés sur un carnet d'épargne pendant 6 ans à 4,5 % (on retire les intérêts chaque année).
C0 = 8500
r = 0,045 (attention : 4,5 % ou 45/100)
n = 6
|
CAPITAL
|
INTÉRÊT
|
|
Cn = C0 * ( 1 + n * r )
= 8500 * (1 + 6 * 0,045)
= 10 795
|
in = C0 * n * r
= 8500 * 6 * 0,045
= 2 295
|
|
Je place un capital de 300 € à du 3 % pendant 1 an
300 . 3 . 1
I = ————— = 9 €
100
pendant 5 ans
300 . 3 . 5
I = ————— = 45 €
100
Si je recherche :
C . r . n
I = —————
100
100 . I
C = —————
r . n
100 . I
r = —————
C . n
I . 100
n = —————
C . r
|
Je place un capital de 300 € à un taux de 2,5 %
pendant 6 mois.
300 . 2,5 . 6
I = —————— = 3, 75 €
100 . 12
pendant 3 mois
300 . 2,5 . 3
I = —————— = 1, 88 €
100 . 12
Si je recherche :
C . r . n
I = —————
100 . 12
100 . 12. I
C = ——————
r . n
100 . 12. I
r = ——————
C . n
I . . 12 . 100
n = ——————
C . r
|
Je place 300 € à du 3 % pendant 60 jours
300 . 3 . 60
I = —————— = 1 ,5 €
100 . 360
pendant 95 jours
300 . 3 . 95
I = —————— = 2,38 €
100 . 360
Si je recherche :
C . r . n
I = —————
100 . 360
100 . 360. I
C = ——————
r . n
100 . 360. I
r = ——————
C . n
I . . 360 . 100
n = ——————
C . r
|
| Fanny a placé un capital de 6500 € à du 4,5 % sur un compte à terme pendant 8 ans. Calcule l’intérêt à la fin du terme. |
C = 6500
I = ?
n = 8
r = 4,5
|
C . r . n 6500 . 4,5. 8
Formule : I = ————— = ———————— = 2340 €
100 100
|
Après 10 ans de placement, le capital de Laure, soit 12500 € a rapporté 5000 € d’intérêts. A quel taux Laure avait-elle placé l’argent ?
|
C = 1250
I = 5000
n = 10
r = ? |
C . r . n
Formule : I = ————— 100 . I = C . r . n
100
100 . I 100 . 500
r = ————— = ————————— = 4%
C . n 1250 . 10 |
Elise possède 600 €. Combien de temps doit-elle laisser la somme placée sur son livret d’épargne (4%) pour que l’intérêt rapport 600 € ?
|
C = 600
I = 600
n = ?
r = 4% |
C . r . n
Formule : I = ————— ===> 100 . I = C . r . n
100
100 . I 100 . 600
n = ————— = ————————— = 25 ans
C . r 600 . 4 |
Quelle somme dois-tu placer en banque à du 5,5 % pour qu’elle te rapporte un intérêt annuel de 14850 € ?
|
C = ?
I = 14850
n = 1 an
r = 5,5 % |
C . r . n
Formule : I = ————— ===> 100 . I = C . r . n
100
100 . I 100 . 14850
C = ————— = ————————— = 270000 €
n . r 5,5 . 1 |
Louise a laissé 520 € sur un compte d’épargne à du 3,25 % pendant 9 mois. Combien va-t-elle toucher d’intérêts ?
|
C = 520
I = ?
n = 9 mois
r = 3,25 % |
C . r . n (mois)
Formule : I = ———————— ===> 12. 100 . I = C . r . n
100 . 12
r . C . n 3,25 . 520 . 9
I = ————— = ————————— = 12 , 68 €
100 . 12 100 . 12 |
Mon compte à vue est en négatif de 1115 € depuis 78 jours. Quelle somme vais-je devoir rembourser à la banque pour ce découvert ? (14 %)
|
C = 1115 €
I = ?
n = 78 jours
r = 14 % |
C . r . n (jours)
Formule : I = ———————— ===> 360 . 100 . I = C . r . n
100 . 360
r . C . n 14 . 1115 . 78
I = —————— = ————————— = 33, 82 €
100 . 360 100 . 360
Je dois rembourser le découvert + les intérêts soit
1115 + 33,82 = 1148,82 €
|
Complète le tableau ci-dessous.
| |
Capital |
Taux |
Durée |
Intérêts |
| 1 |
10.000,00 € |
5 % |
6 ans |
3.000,00 € |
| 2 |
5.000,00 € |
8 % |
123 jours |
13,67 € |
| 3 |
150.000,00 € |
5 % |
3 mois |
1.875,00 € |
| 4 |
2.000,00 € |
2,5 % |
1 an |
50,00 € |
|
d'après une préparation trouvée sur www.enseignons.be
2. Confusion intérêt (i) et taux d'intérêt (r).
i = intérêt = ici : 8500 * 0,045 = 382,5 € (par an)
r = taux = ici : 0,045 ou 4,5 % ou 45/100
II. Intérêts composés
-
définition
-
exemple introductif
-
démonstration ou monstration ?
-
Exemples chiffrés
Quelle est la valeur acquise par 8500 €, placés sur un carnet d'épargne pendant 6 ans à 4,5 % // Quelle est la valeur acquise par 8500 €, placés en bons de capitulation pendant 6 ans à 9 % (taux brut... donc 8,1 % net en début 93, devenant 7,7949 % net après le 01-01-94 et 7, 65 % depuis le 01-01-97... variation du précompte mobilier // et si le placement est fait pendant 5 ans et 7 mois ?
-
problèmes dérivés
Quelle somme faut-il placer à intérêts composés, pour obtenir Cn aprè n années ? // À quel taux faut-il placer à intérêts composés la somme Co pour obtenir Cn après n années ? // Pendant combien de temps dois-je placer au taux r, à intérêts composés, la somme Co pour obtenir le montant Cn ?
A. Définition
Un capital est placé à intérêts composés quand, à la fin de chaque période, les intérêts s'ajoutent au capital, pour produire aussi des intérêts.
B. Exemple introductif
|
CAPITAL
|
INTÉRÊT
|
|
Je place 10000 € pendant 10 ans...à 10 %
mon capital devient :
an 0 : 10000
an 1 : 10000 + 1000 = 11000
an 2 : 11000 + 1100 = 12100
an 3 : 12100 + 1210 = 13310
an 4 : 13310 + 1331 = 14641
etc...
|
Je place 10000 € pendant 10 ans...à 10 %
mon intérêt devient :
an 0 : 0
an 1 : 1000
an 2 : 2100
an 3 : 3310
an 4 : 4641
etc...
|
C. Démonstration ou monstration ?
|
CAPITAL
|
INTÉRÊT
|
|
C0 = capital de départ
Ci = capital à la ie période
Cn = capital à la ne période
r = taux d'intérêt (rate)
n = durée du placement en période
* première année
C1 = capital + intérêt
= C0 + C0 * r
= C0 * ( 1 + r )
* deuxième année
C2 = capital + intérêt
= C1 + C1 * r
= C1 * ( 1 + r )
= C0 * ( 1 + r ) * ( 1 + r )
= C0 * ( 1 + r )2
* ne année
Cn = capital + intérêt
= Cn-1 + Cn-1 * r
= Cn-1 * ( 1 + r )
= C0 * ( 1 + r )n-1 * ( 1 + r )
= C0 * ( 1 + r )n
|
C0 = capital de départ
Ii = intérêt de la ie période
In = intérêt de la ne période
r = taux d'intérêt (rate)
n = durée du placement en période
* première année
I1 = intérêt
= C0 * r
=
* deuxième année
I2 = C2 - C0
= C0 * ( 1 + r )2 - C0
= C0 * [( 1 + r)2 - 1]
=
=
* ne année
In = Cn - C0
= C0 * ( 1 + r )n - C0
= C0 * [ ( 1 + r )n - 1]
=
=
|
D. Exemples chiffrés
1. Quelle est la valeur acquise par 8500 €, placés sur un carnet d'épargne pendant 6 ans à 4,5 %.
C0 = 8500
r = 0,045 (attention : 4,5 %)
n = 6
Cn = C0 * ( 1 + r )n
= 8 500 * 1,0456
= 11 069,2 €
In = [ C0 * ( 1 + r )n - 1]
ou = 11 069,2 - 8 500
= 2 569,2 €
2. Quelle est la valeur acquise par 8500 €, placés en bons de capitulation pendant 6 ans à 9 % (taux brut... donc 8,1 % net en début 93, devenant 7,7949 % net après le 01-01-94 et 7,65 % depuis le 01-01-97...variation du précompte mobilier).
C0 = 8500
r = 0,081 (attention : 8,1 %)
n = 6
Cn = C0 * ( 1 + r )n
= 8500 * 1,0816
= 13563,5 €
3. Et si le placement est fait pendant 5 ans et 7 mois ??
Il suffit de calculer n = 5 + 7/12 = 5,583
E. Problèmes dérivés
1. Quelle somme faut‑il placer à intérêts composés, pour obtenir Cn après n années ?
on sait que : Cn = C0 * (1+r)n
donc :
Cn = C0
(1+r)n
2. À quel taux faut‑il placer à intérêts composés la somme C0 pour obtenir Cn après n années ?
on sait que : Cn = C0 * (1 + r )n
donc :
Cn / C0 = (1 + r )n
donc :
(Cn/C0)1/n = (1 + r )
donc :
(Cn/C0)1/n ‑ 1 = r
3. Pendant combien de temps dois‑je placer au taux r, à intérêts composés, la somme C0 pour obtenir le montant Cn ?
on sait que : Cn = C0 * (1 + r )n
donc :
Cn / C0 = (1 + r )n
donc :
log (Cn / C0) = log (1 + r )n ]
donc :
log (Cn / C0) = n * log (1 + r )
log (Cn / C0) = n
log (1 + r)
III. Annuités
-
définition
-
démonstration
-
Exemples chiffrés
-
problèmes dérivés
Quel est le montant à placer annuellement, pour obtenir après n versements au taux r, un capital A ? // Quelle est le nombre d'années pendant lesquelles je dois verser un montant pour obtenir A au taux r ?
A. Définition
On appelle annuité, une série de versements égaux (termes) faits annuellement (ou à échéances régulières) soit dans le but de constituer un capital, soit de rembourser une dette.
B. Démonstration
A = la valeur acquise par les versements
a = le montant de chaque versement
r = le taux
n = le nombre de versements
>>On suppose que les versements ont lieu à la fin de chaque terme, le premier à la fin du premier terme, et que le dernier ne rapportera donc pas d'intérêts.
* on sait que A sera la somme de plusieurs versements qui resteront placés à intérêts composés, donc cette somme de n termes :
A = a * (1+r)n‑1 + a * (1+r)n‑2 + a * (1+r)n‑3 + ...+ ...+ a * (1+r)2 + a*(1+r) + a
* si on laisse cette somme placée pendant un an, on aura toujours une somme de n termes :
A*(1+r) = a * (1+r)n + a * (1+r)n-1 + a * (1+r)n‑2 + ... + ...+ a * (1+r)2 + a*(1+r)
* si on soustrait la première égalité de la deuxième (et oui, la deuxième est plus grande que la première), on aura :
A + A*r - A = a * (1+r)n + a * (1+r)n-1 + a * (1+r)n‑2 + a * (1+r)n‑3 ... + ...+ a * (1+r)2 + a*(1+r)
- a * (1+r)n‑1 - a * (1+r)n‑2 - a * (1+r)n‑3 - ...- ...- a * (1+r)2 - a*(1+r) - a
A + A*r ‑A = a * (1+r)n ‑ a
ou,
A * r = a * [ (1+r)n ‑1 ]
et donc,
A = a * (1+r)n‑1
r
C. Exemple chiffré
Quel capital vais‑je obtenir en plaçant une annuité de 24 000 €, sur un carnet à 6,5 % pendant 15 ans ?
On sait que :
A = a * (1+r)n‑1
r
ou
A = 24000 * [ 1,06515 ‑1 ] / 0,065
ou,
A = 580 372 €
>> À réfléchir : si je versais 2 000 € par mois au lieu de 24 000 € par an...(RÉP: 607 090 €)
D. Problèmes dérivés
1. Quelle est le montant à placer annuellement, pour obtenir après n versements au taux r, un capital A.
* on sait que :
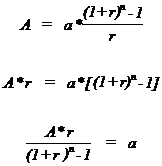
1
|
2. Quel est le nombre d'années pendant lesquelles je dois verser un montant a pour obtenir A au taux r ?
* on sait que :
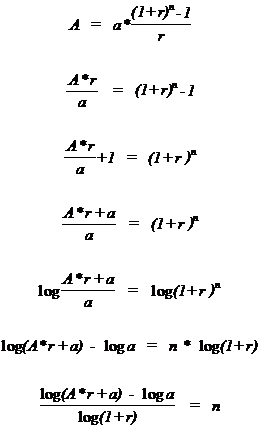
2
|
IV. Emprunts
-
démonstration
-
problèmes dérivés (plus fréquent)
-
le taux de chargement, quelle tromperie !
Quel est le versement annuel, si j'emprunte V au taux r pendant n années ? // Quel remboursement annuel pour emprunter 1 million en 20 ans à 11 % ?
A. Démonstration
* Contrairement au placement par annuités pour obtenir un capital A dans n années, il s'agit d'obtenir immédiatement le montant V. V est donc la valeur actuelle (à recevoir aujourd'hui) du montant A (obtenu en versant les annuités, pendant n années).
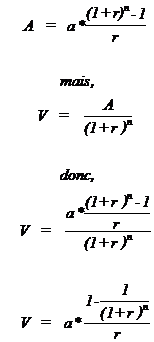
3
|
* Autre démonstration
Je désire emprunter V aujourd'hui.
Pour mon banquier, soit il accepte de me prêter V, et je lui verse chaque année un montant a, soit il refuse de me le prêter et place ce montant V pendant n années.
S'il accepte de me prêter V, je lui verserai un montant a pendant n années ; au bout des n années, il aura obtenu :
A = a * [(1 +r)n+1] / r
Si, par contre, mon banquier refuse de me prêter V aujourd'hui, il va garder ce montant et le placer (plutôt à intérêts composés qu'à intérêts simples ;o). Au bout de n années, il espère que son capital de départ V devienne :
Vn = V * (1+r)n
Quel que soit le choix du client et du banquier, le banquier espère obtenir la même chose au terme des n années prévues, donc :
a * [(1 +r)n-1] / r = V * (1+r)n
Et donc,
a * [(1 +r)n-1] / r = V
(1+r)n
ou mieux,
a * [1-1/(1+r)n ] = V
r
ou, formule dérivée,
a = V * r
[1-1/(1+r)n ]
Cette formule établit bien que l'annuité est constante durant toute la durée de l'emprunt, et que l'intérêt à payer n'est calculé que sur le "solde restant dû".
Au début du remboursement, la part d'intérêt est forte (il reste beaucoup à rembourser) ; cette part d'intérêt va en diminuant (puisque le montant à rembourser diminue) et le dernier remboursement ne comprend presque plus d'intérêt (presque tout est remboursé).
À contrario, puisque l'annuité (ou la mensualité) est constante, la part de capital remboursée à chaque versement va en augmentant...
Bref, ceci confirme un adage généralement connu : "au début on ne rembourse que des intérêts, le capital n'est remboursé qu'à la fin".
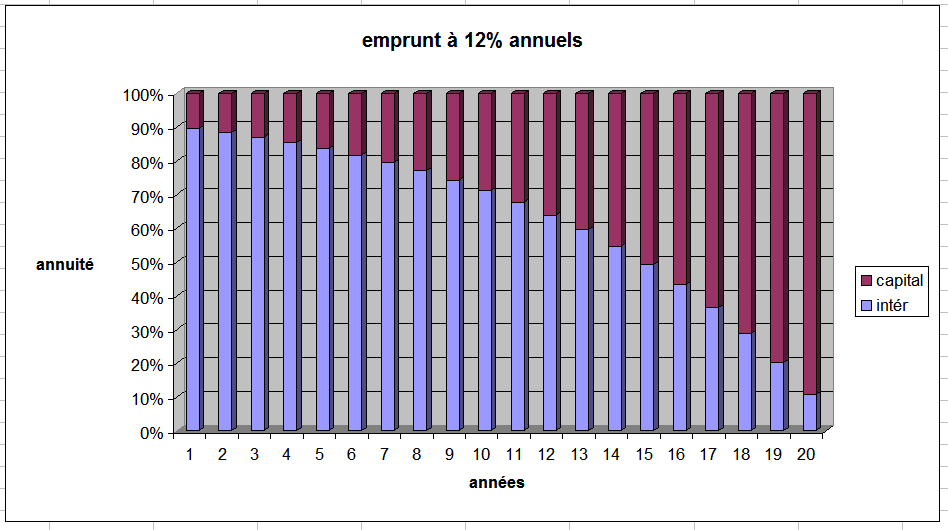
Ainsi, en supposant un emprunt de 100 000 €, pendant 20 ans à un taux annuel de 12 %, cela donnerait une annuité de 13 387,88 € ainsi selon les années :
année
nov-08
nov-09
nov-10
nov-11
nov-12
nov-13
nov-14
nov-15
nov-16
nov-17
nov-18
nov-19
nov-20
nov-21
nov-22
nov-23
nov-24
nov-25
nov-26
nov-27
|
intér
12 000,00
11 833,45
11 646,92
11 438,01
11 204,03
10 941,96
10 648,45
10 319,72
9 951,54
9 539,18
9 077,34
8 560,07
7 980,74
7 331,88
6 605,16
5 791,24
4 879,64
3 858,65
2 715,14
1 434,42
167 757,56 |
capital
1387,88
1554,42
1740,95
1949,87
2183,85
2445,92
2739,43
3068,16
3436,33
3848,70
4310,54
4827,80
5407,14
6056,00
6782,72
7596,64
8508,24
9529,23
10 672,73
11 953,46
100 000,00 |
On constate que la 1re année,
l'intérêt est de 12 000 €, soit 12 % du capital emprunté et encore dû (100 000 €),
le reste de l'annuité constante (soit 1 387,88 €) est affectée au remboursement de capital (très faible).
La onzième année,
le capital restant dû en début d'année sera encore de 75 644,50 €,
l'intérêt de 12% sur ce solde restant dû est de 12 %, soit 9 077,34 €,
le reste de l'annuité servira au remboursement de capital, soit 4 310,54 €.
La dernière année,
le capital restant dû est de 11 953,46 €,
surlequel un intérêt de 12 % est toujours calculé, soit 1 434,42 € ;
le total des deux donne toujours la même annuité.
|
B. Problème dérivé (plus fréquent)
1. Quel est le versement annuel, si j'emprunte V au taux r pendant n années ?
* on sait que :
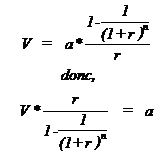
4
|
2. Quel remboursement annuel pour emprunter 1 million en 20 ans à 11 % ?
a = V * r .
[1‑1/(1+r)n]
= 1 000 000 * 0,11 / (1‑1/1,1120)
= 125 576 € par an
>>À réfléchir : cela revient‑il au même que de verser le douzième, soit 10 465 € par mois ? (RÉP: 10 322 €)
3. Le taux de chargement, quelle tromperie !
a. présentation du taux de chargement
Contrairement à la formule de l'emprunt vue ci-dessus, dans le cas d'un emprunt calculé avec taux de chargement, on part de l'idée que :
(1) la part de capital est constante [le capital divisé par le nombre de versements à effectuer] ;
(2) l'intérêt est constant, mais non pas calculé sur le "solde restant dû", mais sur le capital emprunté.
Illustrons par un exemple :
reprenons l'exemple pris ci-dessus, à savoir un emprunt de 100 000 €, pendant 20 ans à un taux annuel de 12 %, qui donnait une annuité de 13 387,88 €, ventilée selon les années en partie capital (faible au début, fort à la fin) et en partie intérêts (fort au début, faible à la fin) ;
comme le taux de chargement est un taux mensuel sur le capital de départ, nous choisirons évidemment 1 %.
Le calcul de l'annuité se fera rapidement :
pour le capital,
100 000 € à rembourser en 20 ans, soit 5 000 € ;
pour l'intérêt,
par mois, 1 % calculé sur 100 000, soit 1 000 par mois ou 12 000 par an ;
l'annuité totale étant de 17 000 €.
Le lecteur aura vite compris la supercherie du taux de chargement, devenu illégal en Belgique.
b. première analyse de la supercherie du taux de chargement
Pour la première année, l'intérêt calculé de 12 000 correspond bien aux 12 % annuels sur les 100 000 € ...
Après 5 ans, calculer 12 000 d'intérêt pour la sixième année, alors que le capital restant dû n'est plus que 100 000 au départ, diminué de 5 remboursements de capital de 5 000 par an, soit 100 000 - 25 000, ou encore 75 000 €... ça commence à faire cher comme intérêt (12 000/75 000 = 16 %).
Après 10 ans, calculer 12 000 d'intérêt pour la onzième année, alors que le capital restant dû n'est plus que 100 000 au départ, diminué de 10 remboursements de capital de 5 000 par an, soit 100 000 - 50 000, ou encore 50 000 €... c'est de plus en plus cher comme intérêt (12 000/50 000 = 24 %).
Après 15 ans, calculer 12 000 d'intérêt pour la seizième année, alors que le capital restant dû n'est plus que 100 000 au départ, diminué de 15 remboursements de capital de 5 000 par an, soit 100 000 - 75 000, ou encore 25 000 €... ça devient trop cher comme intérêt (12 000/25 000 = 48 %).
Mais calculer 12 000 d'intérêt pour la dernière année, alors que le capital restant dû n'est plus que 100 000 au départ, diminué de 19 remboursements de capital de 5 000 par an, soit 100 000 - 95 000, ou encore 5 000 €... ce n'est pas cher comme intérêt, c'est un intérêt intolérable (12 000/5 000 = 240 %).
e. deuxième essai de correction de la supercherie du taux de chargement : la durée réelle
Ce taux de chargement était un mauvais calcul, car il est calculé sur le montant total de l'emprunt, sans tenir compte, qu'au fur et à mesure des mois qui passent, le capital va en diminuant, donc, les intérêts devraient aller en diminuant.
D'où l'idée (une parmi d'autres) de faire un calcul de durée réelle.
12000, intérêt à payer sur 20 ans,
11400, intérêt à payer sur 19 ans,
10800, intérêt à payer sur 18 ans,
10200, intérêt à payer sur 17 ans,
9600, intérêt à payer sur 16 ans,
9000, intérêt à payer sur 15 ans,
8400, intérêt à payer sur 14 ans,
7800, intérêt à payer sur 13 ans,
7200, intérêt à payer sur 12 ans,
6600, intérêt à payer sur 11 ans,
6000, intérêt à payer sur 10 ans,
5400, intérêt à payer sur 9 ans,
4800, intérêt à payer sur 8 ans,
4200, intérêt à payer sur 7 ans,
3600, intérêt à payer sur 6 ans,
3000, intérêt à payer sur 5 ans,
2400, intérêt à payer sur 4 ans,
1800, intérêt à payer sur 3 ans,
1200, intérêt à payer sur 2 ans,
600, intérêt à payer sur 1 an,
En prenant la première année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 2e et la 20e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 3e et la 19e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 4e et la 18e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 5e et la 17e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 6e et la 16e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 7e et la 15e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 8e et la 14e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 9e et la 13e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant la 10e et la 12e année, c'est comme si on empruntait 12000 € pendant 1 an
En regroupant le 11e et le 11e année, c'est comme si on empruntait pendant 1 année,
mais il n'y a qu'une seule 11e année, donc c'est comme si l'on empruntait pendant 0,5 année.
La durée moyenne (baptisée durée réelle) sera donc de (20+1)/2 soit 10,5 années au lieu des 20 initialement calculées,
ou bien 10 * 1 année + 1 fois une demie année.
Les années manquantes ne disparaissent pas, mais on considère l'emprunt et les intérêts à payer réellement sur 13,5 années au lieu des 20 années.
f. troisième essai de correction de la supercherie du taux de chargement : la formule de correction
Il existe aussi une formule approximative de correction... elle permet de calculer le TAEG (ou TEG) en connaissant le taux de chargement :
taux réel = Taux de chargement (mensuel) x 24 x nombre de périodes
(nombre de périodes + 1)
Dans le cas de l'emprunt présenté ci-dessus au taux de chargement de 12 % l'an, on aurait :
TAEG = 0,01 * 24 * 20 / 21, soit 22,86 %
V. En résumé
Synthèse des formules
|
Intérêts simples
Cn = C0 . (1+n.r)
|
Intérêts composés
Cn = C0 . (1+r)n
r = ( Cn/C0)1/n – 1
n = log (Cn/C0)
log (1+r)
|
Annuités
A = a . (1+r)n – 1
R
a = A . r
(1+r)n – 1
n = log (A . r +a) –log a
log (1+r)
|
Emprunts
V = a . 1-1/(1+r)n
r
a = V . r
1-1/(1+r)n
|
VI. Exercices
I. Déterminer la valeur acquise par un capital de 123.000 EUR placé à intérêts composés de 8,75 % :
a) pendant 8 ans ;
b) pendant 7 ans et 3 mois.
RÉPONSE : a) 240 624 EUR b) 225 953 EUR
II. Quelle est la somme acquise par 75 000 EUR placé à 5 % :
a) pendant 6 ans ;
b) pendant 7 ans et demi ;
c) pendant 9 ans et 5 mois.
RÉPONSE : a) 100 507 EUR b) 108 139 EUR c) 118 739 EUR
III. Les intérêts étant capitalisés tous les trimestres sur un compte à 6 %, que vaudra après 13 ans et 6 mois, une somme de 125 000 EUR ?
RÉPONSE : 279 303 EUR
IV. Calculer la somme qu'il faut placer à 9 % pour obtenir 100 000 EUR après :
a) 10 ans ;
b) 15 ans ;
c) 20 ans.
RÉPONSE : a) 42 241 EUR b) 27 454 EUR c) 17 843 EUR
V. Quelle somme faut‑il placer à intérêts composés pour obtenir, 12 ans après, 250 000 EUR :
a) au taux de 3,5 %
b) au taux de 4,5 %
c) au taux de 6 %
d) au taux de 7,5 %
e) au taux de 9 %
RÉPONSE : a) 165 446 EUR b) 147 416 EUR
c) 124 242 EUR d) 104 964 EUR e) 88 884 EUR
VI. Combien de temps faut‑il placer la somme de 1 000 000 EUR au taux de 6 % (composés), pour obtenir :
a) 1 304 770 EUR
b) 1 500 000 EUR
c) 2 000 000 EUR
d) 3 000 000 EUR
RÉPONSE : a) 4,5655 ans b) 6,9585 ans c) 11,8957 ans d) 18,8542 ans
VII. Un capital c étant placéau taux annuel r , pendant n années, représenter graphiquement la valeur acquise par c en fonction de n :
a) dans le cas d'intérêts simples ;
b) dans le cas d'intérêts composés.
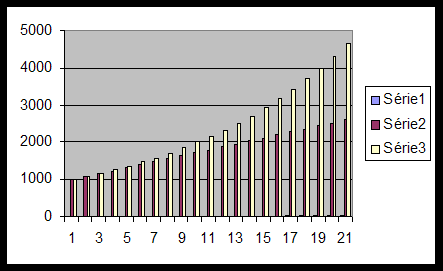
exemple sur 20 ans à 8 % l'an
VIII. Un capital c étant placéau taux annuel r , montrer que les valeurs acquises après 1, 2, 3... n années forment une progression :
a) arithmétique, dans le cas d'intérêt simple ;
b) géométrique, dans le cas d'intérêts composés.
a1) Cn = C0 + n * r * C0
IX. Après combien de temps un capital, placé:
a) à 4 % à intérêts simples est-il doublé ?
b) à 8 % à intérêts simples est-il doublé ?
c) à 4 % à intérêts composés est-il doublé ?[21]
d) à 8 % à intérêts composés est-il doublé ?
e) à 4 % à intérêts simples est-il quadruplé ?
f) à 8 % à intérêts simples est-il quadruplé ?
g) à 4 % à intérêts composés est-il quadruplé ?
h) à 8 % à intérêts composés est-il quadruplé ?
RÉPONSE : a) 25 ans b) 12,5 ans c) 17,67 ans d) 9,0065 ans
e) 75 ans f) 37,5 ans g) 35,35 ans h) 18,129 ans
X. Soit une somme de 5 000 EUR placée à 7 % ; qu'est-elle devenue après 4 ans ? À quel moment cette somme devient-elle égale à 40 000 EUR ?
RÉPONSE : Après 4 ans :
C4 = C0 . (1 + r)4
C4 = 5 000 . (1 + 0,07)4
C4 = 6 554
Moment où Cn = 40 000
40 000 = C0 . (1 + r)x
40 000 = 5 000 . (1 + 0,07)x
8 = (1,07)x
log 8 = log (1,07)x
log 8 = x log (1,07)
x = 30,7
Il faudra 31 ans pour obtenir 40 000 EUR
XI. Dans 7 ans, je pourrai disposer d'une somme de 1 000 000 EUR. À quelle somme actuelle ce montant correspond-il si l'inflation est de :
a) 4 %
Réponse : 759 918
b) 8 %
583 490
c) 10 %
513 158
d) 12 %
452 349
XII. Une somme de 3 000 000 EUR m'est payable dans 15 ans ; calculer sa valeur (taux moyen d'inflation : 4 % ) :
a) aujourd'hui ;
b) dans 3 ans ;
c) dans 5 ans ;
d) dans 10 ans ;
e) dans 12 ans et 7 mois.
RÉPONSE : a) 1 665 794 b) 1 873 791
c) 2 026 693 d) 2 465 781 e) 2 728 710
XIII. Même question, si l'inflation passe à 8 %.
RÉPONSE : a) 945 725 b) 1 191 341
c) 1 389 580 d) 2 041 750 e) 2 490 848
XIV. Pour une propriétémise en vente, un client A m'offre 2 000 000 EUR immédiatement ; B offre 2 360 000 EUR à payer dans trois ans et C offre 2 836 500 EUR payables dans 6 ans. Si je peux placer mon argent à 6 %, quelle est l'offre la plus intéressante ?
RÉPONSE calculée en euros futurs de 6 ans plus tard :
a) 2 837 038 b) 2 810 798 c) 2 836 500 : a est le meilleur
à refaire en euros actuels
XV. Un industriel engage 20 000 000 EUR dans une affaire ; deux ans plus tard, il en retire 22 500 000 EUR. Quel est le taux de placement réalisé ?
RÉPONSE : 6,06 %
XVI. Même question pour celui qui retire 15 000 000 EUR d'une affaire où il a engagé la somme de 9 000 000 EUR 5 ans plus tôt.
RÉPONSE : 10,75 %
XVII. Un capital double en 2 ans. Quel est le taux du placement ?
RÉPONSE : 41,42 %
XVIII. Au Pérou, il est possible de placer son argent sur un carnet qui rapporte du 57 %. Combien de temps faut-il pour que son argent placé soit multiplié par 20 ?
RÉPONSE : 6,64 ans
XIX. Combien dois-je mettre sur le carnet d'épargne (6 %) de mes enfants à leur naissance, si je veux qu'ils aient 300 000 EUR à leur majorité (=18 ans) ; et si je souhaite qu'ils aient cette somme à 25 ans.
RÉPONSE : 105 103 EUR ; 69 900 EUR
XX. Je devais payer 60 000 dans 2 ans et la même somme dans 5 ans. Malheureusement, bien que j'ai l'argent, je ne serai en mesure de payer que dans 8 ans, aux héritiers. Combien devrais-je débourser à ce moment-là ? (taux 6,5 %)
RÉPONSE : 160 026 EUR
XXI. Je dois payer 240 000 EUR dans 7 ans et j'ai la possibilité de placer mon argent à 8 %. Combien dois-je placer aujourd'hui pour régler ma dette dans 7 ans ?
RÉPONSE : 140 038 EUR
XXII. Je dois payer 240 000 EUR dans 7 ans et j'aurai la possibilitéde placer mon argent à 8 %. Combien dois-je placer dans 3 ans pour régler ma dette dans 7 ans ?
RÉPONSE : 176 407 EUR
XXIII. Je devrai payer 240 000 EUR dans 7 ans et 120 000 EUR dans 9 ans et j'ai la possibilité de placer mon argent à 8 %. Combien dois-je placer aujourd'hui pour régler mes dettes en leur temps ?
RÉPONSE : 140 038 + 60 030, soit 200 068 EUR
XXIV. Je dois payer 240 000 EUR dans 7 ans et 120 000 EUR dans 9 ans et j'aurai la possibilité de placer mon argent à 8 % dans 2 ans. Combien dois-je placer dans 2 ans pour régler mes dettes dans 7 et 9 ans ?
RÉPONSE 1ère façon : 163 340 + 70 019, soit 233 359 EUR
2e façon : 200 068 * 1,082, soit 233 359 EUR
XXV. Un capital est de 10 000 000 EUR est placé à intérêts composés. On sait que si on le laissait placé un an de plus, il serait augmenté de 449 946 EUR ; et si on le laissait 2 ans de plus, il serait à nouveau augmenté de 467 943 EUR.
Trouver le taux et la durée initiale de ce placement.
IGNORÉS : le taux ; la durée initiale ; la durée un an de plus ; la durée 2 ans de plus ; le montant acquis à l'échéance initiale ; le montant acquis un an plus tard ; le montant acquis 2 ans plus tard
CHOIX DE(s) L'INCONNUE(s) : x = le montant acquis à l'échéance "initiale" ; r = le taux
EXPRESSION DES DONNÉES :
le taux = r
le montant 1 an plus tard = x + 449 946 ou x (1+r)
le montant 2 ans plus tard = x + 917 889 ou x (1+r)2 ou (x+449 946)(1+r)
MISE EN ÉQUATION :
x + 917 889 = x (1+r)2 = (x+449 946)(1+r)
ce qui forme un système de 2 équations à 2 inconnues
RÉSOLUTION :
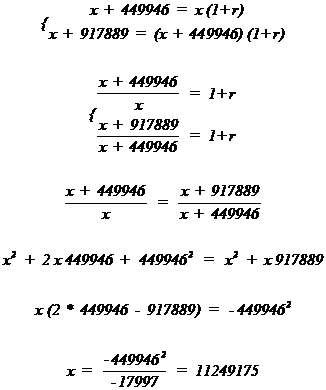
6
|
RÉPONSE :
la somme de départ est devenue 11 249 175 EUR ;
donc r = 0,04 soit 4 %
et la durée de placement initiale était de 3 ans.
XXVI. Deux sommes égales sont placées, l'une depuis 28 ans à 4,5 % et l'autre depuis 24 ans à 5 % . Ensemble, elles valent aujourd'hui 133 096 EUR. Quelles sont ces sommes?
IGNORÉS : la première somme de départ ; la deuxième somme de départ ; le montant acquis à l'échéance par la première somme ; le montant acquis 4 ans plus tôt par la seconde somme ;
CHOIX DE(s) L'INCONNUE(s) : x = le montant acquis par la première somme (placée 28 ans), à l'échéance ;
EXPRESSION DES DONNÉES :
ce montant au départ = x .
(1+0,045)28
le montant acquis par la seconde somme = 133096 - x
ce montant au départ = 133096 - x
(1+0,05)24
MISE EN ÉQUATION :
RÉSOLUTION :
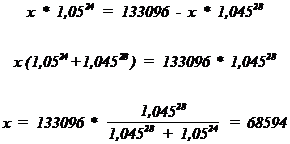
8
|
RÉPONSE :
la première somme est devenue 68 594 EUR ;
donc l'autre est donc devenue 133 096 - 68 594 soit 64 502 EUR
et, au départ, ces sommes étaient, ou 68 594 / 1,04528, ou 64 502 / 1,0524 soit 20 000 EUR.
XXVII. Pour la vente de ma villa, trois candidats se présentent : A offre 2 millions tout de suite ; B offre 2 320 000 EUR dans 4 ans et C disposera de 2 140 000 EUR dans 6 mois. Quelle est la meilleure offre, sachant que je peux placer mon argent à 5 % .
RÉPONSE calculée en francs futurs de 4 ans plus tard :
a) 2 431 012 c) 2 538 495 b) 2 320 000 ==>C est le meilleur
à refaire en francs actuels
XXVIII. Un oncle d'Amérique meurt et laisse une fortune de 25 661 000 EUR. Dans ses dernières volontés, il souhaite que ses trois neveux, âgés aujourd'hui de 13, 14 et 16 ans, aient la même chose le jour de leur anniversaire de 21 ans et qu'en attendant, l'argent reste placésur un compte qui rapporte 5 %. Quelle est la part de chacun ?
IGNORÉS : la première part au départ ; la deuxième part au départ ; la troisième part au départ ; la première part distribuée, la deuxième part distribuée ; la troisième part distribuée ;
CHOIX DE(s) L'INCONNUE(s) : x = le montant (identique) des parts distribuées aux différents anniversaires ;
x0, y0 et z0 les montants que représentaient ces parts distribuées, au moment du décès.
EXPRESSION DES DONNÉES :
ce montant distribué, valait au départ = x0 ou y0 ou z0
(1+0,05)13 1,0514 1,0516
donc, y0 = x0 1,0514 et z0 = x0 1,0516
(1,05)13 (1,05)13
MISE EN ÉQUATION :
la somme de ces parts valait 25 661 000 au moment du décès, donc
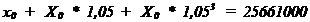
9
|
RÉSOLUTION :
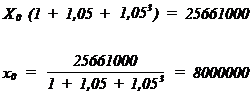
10
|
RÉPONSE :
le premier 8 000 000 EUR, qui sont devenus 8 ans plus tard 11 819 644 ;
le deuxième 8 400 000 EUR, qui sont devenus 7 ans plus tard 11 819 644 ;
le troisième 9 261 000 EUR, qui sont devenus 5 ans plus tard 11 819 644 EUR ;
la somme, au moment du décès est bien de 25 661 000 EUR
XXIX. Pendant 30 ans, on place annuellement 15 000 EUR à 6 % .
a) Quel est le capital constitué après la dixième année?
b) " " " " " vingtième " ?
c) " " " " " trentième " ?
RÉPONSE : a) 197 712 b) 551 784 c) 1 185 873
XXX. Même problème, si l'on place cette somme en début de chaque année au lieu de les placer en fin de chaque année.
RÉPONSE : a) 209 575 b) 584 891 c) 1 257 025
XXXI. Je dois rembourser une dette et verse chaque année 150 000 EUR. Quel capital aurais‑je pu avoir après 20 ans, si j'avais pu placer cet argent en vue d'une épargne personnelle au taux de 9 % ?
RÉPONSE : 7 674 018
XXXII. Quel capital dois‑je verser en fin de chaque année pour constituer un capital de 1 500 000 EUR dans dix ans, au taux de 8,5 % ?
RÉPONSE : 101 111 EUR
XXXIII. Une personne doit s'acquitter de 6 termes annuels de 10 000 EUR. Elle désire s'acquitter dès le premier versement en une seule fois. Quel est le montant du versement à effectuer ce jour‑là ?
RÉPONSE : problème impossible, il manque un taux d'intérêt ; imaginons 10 %
valeur future de ces versements :
valeur actuelle de ces 6 versements futurs :
valeur l'an prochain de cette valeur actuelle :
XXXIV. Pendant combien de temps dois‑je épargner 12 000 EUR par an, pour pouvoir m'acheter une moto de 70.000 EUR, si je place mon argent à 6 % ?
RÉPONSE : 5,15 ans, c-à-d 5 ans et 55 jours
XXXV. Je verse 12.000 EUR par an, sur mon carnet à 6 % pendant 18 ans.
a) Combien aurai‑je lors du dernier versement ?
b) Combien aurais‑je eu si j'avais versé1 000 EUR par mois ?
RÉPONSE : 370 868 EUR ; 387 353 EUR
XXXVI. J'ai appris qu'une vieille personne avait voulu se constituer un capital de 300 000 EUR par des annuités de 50 000 EUR chacune à 3,5 % . Dans combien d'années aura‑t‑elle constituer ce capital ?
RÉPONSE : 5,541 ans ; c-à-d
XXXVII. Une personne place à la fin de chaque mois, pendant 25 mois la somme de 3 000 EUR. Le vingt‑sixième mois, elle retire 6 000 EUR, puis continue ses versements pendant les 10 mois qui suivent. Calculer ce qui lui reste, si elle place son argent sur un compte à 7,5 % annuels, mais dont les intérêts sont capitalisés tous les mois.
RÉPONSE : A des 25 premiers versements : 203 933
(A-6000) placés pendant 10 mois (r/12 ; 10 m) :
A des 10 derniers versements :
autre méthode : A de 35 versements :
6000 non placés les 10 derniers mois :
XXXVIII. Un emprunt de 2 000 000 EUR est remboursable en 20 ans à 9,5 %. Quel montant vais‑je devoir verser annuellement ?
RÉPONSE : 226 953 EUR
XXXIX. Une ville emprunte la somme de 100 000 000 EUR à rembourser mensuellement en 10 ans au taux de 7,5 % . Quelle somme faut‑il prévoir au budget annuel pour ce remboursement ?
RÉPONSE : 14 244 216 EUR
XL. La ville du problème précédent décide de rembourser tous les ans. Combien faut‑il prévoir au budget annuel ?
RÉPONSE : 14 568 593 EUR
XLI. Une personne emprunte 1 800 000 EUR à 11 % pour vingt ans, versements mensuels. Après dix ans, elle souhaite rembourser le solde de sa dette par un versement unique. Quel est le montant de ce versement ?
RÉPONSE : valeur future de ces 120 premiers versemen/ts :
valeur de départ de ces 120 versements futurs :
différence à verser :
XLII. Même question si elle voulait s'acquitter du solde de sa dette après quinze ans de versements.
RÉPONSE : valeur future de ces 180 premiers versements :
valeur de départ de ces 180 versements futurs :
différence à verser :
XLIII. Représente graphiquement la part de capital et d'intérêt dans le cas d'un remboursement de 1 000 000 EUR à 8 % pendant vingt ans.
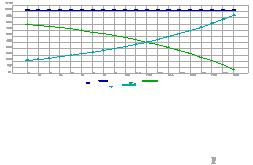
1
|
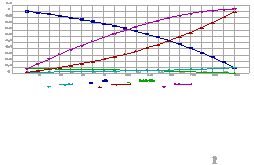
2
|
| an |
dû déb
|
annuité
|
intér
|
capital
|
dû fin
|
cap cumul payé
|
int cumulé
|
| 1 |
1000000,00
|
101852,21
|
80000,00
|
21852,20
|
978147,79
|
21852,20
|
80000,00
|
| 2 |
978147,79
|
101852,21
|
78251,82
|
23600,38
|
954547,40
|
45452,59
|
158251,82
|
| 3 |
954547,40
|
101852,21
|
76363,79
|
25488,41
|
929058,98
|
70941,01
|
234615,61
|
| 4 |
929058,98
|
101852,21
|
74324,71
|
27527,48
|
901531,49
|
98468,50
|
308940,33
|
| 5 |
901531,49
|
101852,21
|
72122,51
|
29729,68
|
871801,81
|
128198,18
|
381062,85
|
| 6 |
871801,81
|
101852,21
|
69744,14
|
32108,06
|
839693,74
|
160306,25
|
450806,99
|
| 7 |
839693,74
|
101852,21
|
67175,49
|
34676,70
|
805017,03
|
194982,96
|
517982,49
|
| 8 |
805017,03
|
101852,21
|
64401,36
|
37450,84
|
767566,19
|
232433,80
|
582383,86
|
| 9 |
767566,19
|
101852,21
|
61405,29
|
40446,91
|
727119,27
|
272880,72
|
643789,15
|
| 10 |
727119,27
|
101852,21
|
58169,54
|
43682,66
|
683436,61
|
316563,38
|
701958,70
|
| 11 |
683436,61
|
101852,21
|
54674,92
|
47177,27
|
636259,33
|
363740,66
|
756633,62
|
| 12 |
636259,33
|
101852,21
|
50900,74
|
50951,46
|
585307,86
|
414692,13
|
807534,37
|
| 13 |
585307,86
|
101852,21
|
46824,62
|
55027,57
|
530280,29
|
469719,70
|
854359,00
|
| 14 |
530280,29
|
101852,21
|
42422,42
|
59429,78
|
470850,50
|
529149,49
|
896781,42
|
| 15 |
470850,50
|
101852,21
|
37668,04
|
64184,16
|
406666,33
|
593333,66
|
934449,46
|
| 16 |
406666,33
|
101852,21
|
32533,30
|
69318,90
|
337347,43
|
662652,56
|
966982,77
|
| 17 |
337347,43
|
101852,21
|
26987,79
|
74864,41
|
262483,02
|
737516,97
|
993970,57
|
| 18 |
262483,02
|
101852,21
|
20998,64
|
80853,56
|
181629,45
|
818370,54
|
1014969,21
|
| 19 |
181629,45
|
101852,21
|
14530,35
|
87321,85
|
94307,60
|
905692,39
|
1029499,56
|
| 20 |
94307,60
|
101852,21
|
7544,60
|
94307,60
|
0,00
|
1000000,00
|
1037044,17
|
| |
|
|
|
|
|
|
|
| tot |
|
|
1037044,17
|
1000000,00
|
|
|
|
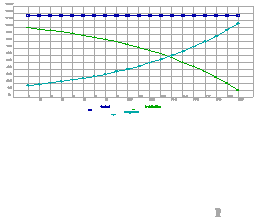
3
|
XLIV. Même question si l'emprunt est à 10 %.
| an |
dû déb
|
annuité
|
intér
|
capital
|
dû fin
|
cap cumul payé
|
int cumulé
|
| 1 |
1000000,00
|
117459,62
|
100000,00
|
17459,62
|
982540,38
|
17469,62
|
100000,00
|
| 2 |
982540,38
|
117459,62
|
98254,04
|
19205,59
|
963334,79
|
36665,21
|
198254,04
|
| 3 |
963334,79
|
117459,62
|
96333,48
|
21126,15
|
942208,64
|
57791,36
|
294587,52
|
| 4 |
942208,64
|
117459,62
|
94220,86
|
23238,76
|
918969,88
|
81030,12
|
388808,38
|
| 5 |
918969,88
|
117459,62
|
91896,99
|
25562,64
|
893407,24
|
106592,76
|
480705,37
|
| 6 |
893407,24
|
117459,62
|
89340,72
|
28118,90
|
865288,34
|
134711,66
|
570046,09
|
| 7 |
865288,34
|
117459,62
|
86528,83
|
30930,79
|
834357,55
|
165642,45
|
656574,93
|
| 8 |
834357,55
|
117459,62
|
83435,76
|
34023,87
|
800333,68
|
199666,32
|
740010,68
|
| 9 |
800333,68
|
117459,62
|
80033,37
|
37426,26
|
762907,43
|
237092,57
|
820044,05
|
| 10 |
762907,43
|
117459,62
|
76290,74
|
41168,88
|
721738,55
|
278261,45
|
896334,79
|
| 11 |
721738,55
|
117459,62
|
72173,85
|
45285,77
|
676452,78
|
323547,22
|
968508,65
|
| 12 |
676452,78
|
117459,62
|
67645,28
|
49814,35
|
626638,43
|
414692,13
|
1036153,93
|
| 13 |
626638,43
|
117459,62
|
62663,84
|
54795,78
|
571842,65
|
428157,35
|
1098817,77
|
| 14 |
571842,65
|
117459,62
|
57184,26
|
60275,36
|
511567,29
|
488432,71
|
1156002,03
|
| 15 |
511567,29
|
117459,62
|
51156,73
|
66302,90
|
445264,39
|
554735,61
|
1207158,76
|
| 16 |
445264,39
|
117459,62
|
44526,44
|
72933,19
|
372331,21
|
627668,79
|
1251685,20
|
| 17 |
372331,21
|
117459,62
|
37233,12
|
80226,50
|
292104,70
|
707895,30
|
1288918,32
|
| 18 |
292104,70
|
117459,62
|
29210,47
|
88249,15
|
203855,55
|
796144,45
|
1318128,79
|
| 19 |
203855,55
|
117459,62
|
20385,55
|
97074,07
|
106781,48
|
893218,52
|
1338514,35
|
| 20 |
106781,48
|
117459,62
|
10678,15
|
106781,48
|
0,00
|
1000000,00
|
1349192,50
|
| |
|
|
|
|
|
|
|
| tot |
|
|
1349192,50
|
1000000,00
|
|
|
|
dû déb annuité intér capital dû fin cap cumul payé int cumulé
1 1000000,00 117459,62 100000,00 17459,62 982540,38 17459,62 100000,00
2 982540,38 117459,62 98254,04 19205,59 963334,79 36665,21 198254,04
3 963334,79 117459,62 96333,48 21126,15 942208,64 57791,36 294587,52
4 942208,64 117459,62 94220,86 23238,76 918969,88 81030,12 388808,38
5 918969,88 117459,62 91896,99 25562,64 893407,24 106592,76 480705,37
6 893407,24 117459,62 89340,72 28118,90 865288,34 134711,66 570046,09
7 865288,34 117459,62 86528,83 30930,79 834357,55 165642,45 656574,93
8 834357,55 117459,62 83435,76 34023,87 800333,68 199666,32 740010,68
9 800333,68 117459,62 80033,37 37426,26 762907,43 237092,57 820044,05
10 762907,43 117459,62 76290,74 41168,88 721738,55 278261,45 896334,79
11 721738,55 117459,62 72173,85 45285,77 676452,78 323547,22 968508,65
12 676452,78 117459,62 67645,28 49814,35 626638,43 373361,57 1036153,93
13 626638,43 117459,62 62663,84 54795,78 571842,65 428157,35 1098817,77
14 571842,65 117459,62 57184,26 60275,36 511567,29 488432,71 1156002,03
15 511567,29 117459,62 51156,73 66302,90 445264,39 554735,61 1207158,76
16 445264,39 117459,62 44526,44 72933,19 372331,21 627668,79 1251685,20
17 372331,21 117459,62 37233,12 80226,50 292104,70 707895,30 1288918,32
18 292104,70 117459,62 29210,47 88249,15 203855,55 796144,45 1318128,79
19 203855,55 117459,62 20385,55 97074,07 106781,48 893218,52 1338514,35
20 106781,48 117459,62 10678,15 106781,48 0,00 1000000,00 1349192,50
1000000,00
XLV. (1) Pendant combien de temps faut‑il rembourser à 7 % annuellement 4 000 000 EUR si les possibilités de paiements sont de 360 000 EUR par an maximum ? (2) Quel montant pourrait‑on emprunter en 20 ans à 10 % , si l'on pense pouvoir payer 25 000 EUR par mois (à recalculer si l'on pense pouvoir payer 300 000 par an) ?
RÉPONSE 1 : 22,23 ans ; RÉPONSE 2 : 3 224 563 EUR ; 3 178 204 EUR
Suggestion de test de Pierre Collie (promo ?) ;
XLVI. Quelle somme faut-il placer à intérêts composés pour obtenir, 12 ans et 3 mois après, 250 000 EUR, au taux de 4,5 % ?
réponse : Cn=Co(1+r)n
Cn=250 000
r=0,045
. n =12+ 3 =144+3 =147=12,25
12 12 12
Co=250 000 =145 803 EUR
(1,045)12,25
XLVII. Àquel taux faut-il placer 320 000 EUR pour obtenir, 7 ans et 9 mois après, la somme de 379 000 EUR ? (intérêts composés)
réponse : Cn=Co(1+r)n
Co=320 000
Cn=379 000
n=7+9 =93 =7,75
12 12
Cn =(1+r)n
Co
1+r=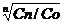 =
=
=1,022
r =1,022-1=0,022=2,2%
3)Quel capital vais-je obtenir en plaçant une annuitéde 2000 EUR par mois, sur un carnet
à 6,2%, pendant 13 ans ?
réponse : A=a (1+r)n-1
r
a=2 000
r= 0,062
12
n=13*12=156
A=2 000..(1+0,062/12)156-1
0,062/12
A=477 791 EUR
XLVIII.Un emprunt de 3 000 000 EUR est remboursable en 25 ans à 8.5% . Quel montant vais-je devoir verser annuellement ?
réponse : V= A
(1+r)n
V=3 000 000
r=0,085
n=25
a = 293 135
XLIX (ou IL ?). Une tante meurt et laisse 21 945 000 EUR. Elle souhaite que ses 3 neveux, âgés aujourd’hui de 12, 16 et 17 ans aient la même somme le jour de leur 21 ans et qu’en attendant, l’argent reste placésur un compte qui rapporte 6,5%. Quelle est la part de chacun ?
réponse : m = le montant identique des parts distribuées aux différents anniversaires
x,y,z = les montants qui représentaient les parts distribuées, au moment du décés
m valait au départ x ou y ou z .
(1,065)12 (1,065)16 (1,065)17
y = x.(1,065)16 z = x.(1,065)17
(1,065)12 (1,065)12
21 945 000 = x+ x(1,065)4+ x(1,065)5
= x(1+(1,065)4+(1,065)5)
x = 21 945 000 . = 6 001 554 EUR
(1+(1,065)4+(1,065)5)
conclusion : le neveu âgéde 12 ans aura 6 001 554 EUR
le neveu âgéde16 ans aura 7 720 797 EUR
le neveu âgéde 17 ans aura 8 222 649 EUR
Ils auront tous à leur 21 ans 10 578 161 EUR.
L. Une personne place durant trois ans 12 000 euros à un taux T1 et 15 000 euros à un taux T2. Le capital total final s'élève à 29 771.87 euros. Si cette personne avait placé durant ces trois ans 12 000 euros au taux T2 et 15 000 euros à un taux T1 alors son capital total final aurait été de 29 752,66 euros.
Déterminer les taux T1 et T2.
Réponse
Il s'agit d'une somme de deux capitalisations pour 3 ans.
La formule de base est Cn = C0 * (1+r)n
12000 * (1+r1)3 + 15000 * (1+r2)3 = 29771,87
et 15000 * (1+r1)3 + 12000 * (1+r2)3 = 29752,66
Isolons (1+r2)3 dans la première équation, pour reporter sa valeur dans la deuxième :
(1+r2)3 = [ 29771,87 - 12000 * (1+r1)3 ] / 15000
et 15000 * (1+r1)3 + 12000 * [ 29771,87 - 12000 * (1+r1)3 ] / 15000 = 29752,66
Cette seconde équation ne contient plus qu'une seule inconnue, r1, donc :
15000 * (1+r1)3 + 12000 * [ 29771,87 - 12000 * (1+r1)3 ] / 15000 = 29752,66
ou 15000 * (1+r1)3 + 0,8 * [ 29771,87 - 12000 * (1+r1)3 ] = 29752,66
ou 15000 * (1+r1)3 + 23817,496 - 9600 * (1+r1)3 = 29752,66
ou 5400 * (1+r1)3 = 29752,66 - 23817,496
ou (1+r1)3 = 5935,164 / 5400 = 1,0991044444444444444444444444444
ou (1+r1) = 1,032
ou r1 = 3,2%
La première équation transformée devient alors :
(1+r2)3 = [ 29771,87 - 12000 * (1+r1)3 ] / 15000
ou (1+r2)3 = [ 29771,87 - 12000 * 1,0991044444444444444444444444444 ] / 15000
=1,1055077777777777777813333333333
ou (1+r2) = 1,034
ou r2 = 3,4%
L'énoncé pouvait nous suggérer que le deuxième taux devait être supérieur au premier, puisqu'en plaçant plus à ce taux, la capitalisation rapportait (un peu) plus.
LI. Pour construire un magasin avec entrepôts, on emprunte 500 000 euros à un taux semestriel de 3 %. On s'engage à rembourser 18 000 euros tous les 6 mois.
a) Après combien d'années la dette est-elle effacée ?
b) À combien faut-il fixer la demi-annuité pour rembourser la dette en 25 ans ?
c) Dans ce dernier cas, combien aurais-je payé à mon banquier (réponse donnée de 3 façons différentes) ?
Réponse a)
Il s'agit d'un remboursement d'emprunt dont on ignore la durée.
or la formule de départ est :
V = a * [1 - (1/(1+r)n] / r
ou
V * r / a = 1 - (1/(1+r)n
ou
V * r / a - 1 = - (1/(1+r)n
ou
1 - V * r / a = + (1/(1+r)n
ou
1 / [1 - V * r / a] = (1+r)n
ou
log {1 / [1 - V * r / a] } = n * log (1+r)
ou
log {1 / [1 - V * r / a] } / log (1+r) = n
ou
log {1 / [1 - 500000 * 0,03 / 18000] } / log (1,03) = n
ou
log {1 / [1 - 0,8333333333...] } / log (1,03) = n
ou
log 6 / log (1,03) = n
ou
n = 0,77815125038364363250876679797961 / 0,012837224705172205171071194580239
= 60,616 semestres soit une bonne trentaine d'années.
Le banquier touchera donc 60,616 * 18000 soit 1 091 088 €
Réponse b) - sans avoir répondu au c préalablement
Il s'agit d'un remboursement d'emprunt dont on connaît la durée, mais on ignore la "semestrialité".
or la formule de départ est :
V = a * [1 - (1/(1+r)n] / r
ou
V * r / [1 - (1/(1+r)n] = a
ou
500000 * 0,03 / [1 - (1/(1,03)50] = a
ou
500000 * 0,03 / [0,77189292021024621642181659821291] = a
ou
19432,75 = a
réponse tout-à-fait acceptable compte tenu de la réponse du a.
Si en payant 18000 par semestre, il fallait une trentaine d'années,
pour arriver à à 25 ans, il faudra accepter de payer plus par semestre...
Réponse c) - méthode 1 : sans avoir répondu au b préalablement
Pour le banquier, il s'agit d'un capital de 500 000 €, à 3 % par semestre pendant 25 ans (soit 50 semestres)
C50 = 500000 * 1,0350 = 2 191 953,01 €
Cette somme inclut les intérêts que percevra le banquier sur les montants perçus et que le banquier replacera... évidemment...
Réponse c) - méthode 2 : après avoir répondu au b
Le banquier aura reçu 50 mensualités de 19432,75 €, soit 971 637,50 €. Ce montant est la vraie réponse à la question, il ne tient pas compte que le banquier va placer ces 'semestrialités' au fur et à mesure qu'il les touchera, et en recevra donc des intérêts.
Réponse c) - méthode 3 : après avoir répondu au b
Le banquier, aura reçu 50 mensualités de 19432,75 €, il les placera au fur et aà mesure de leur réception ce qui engendrera un montant de
A = [a * (1+r)n - 1] / r
= 19432,75 * [ 1,0350 - 1 ] / 0,03
= 19432,75 * 3,3839060187070899052409736192529 / 0,03
= 2 191 953,32 (à quelques centimes près, le même montant qu'en méthode 1)
ou
ou
|
♦ E X E R C I C E S et T R A V A U X
|
-
Introduction
-
Note méthodologique
-
Versement sur son compte postal ou bancaire
-
Retrait de son compte postal/bancaire par chèque/retrait automatique
-
Virement d'un de ses comptes postal/bancaire sur un autre
-
Paiement par chèque/virement bancaire/postal
-
Remise d'un chèque à l'encaissement
-
Remarques diverses
-
Exercices sur les comptes de liaison
I. Secteurs, Catégories et facteurs de production
|
♦ Évaluation des connaissances et des savoir-faire
|
-
Auto-évaluation
-
Évaluation des connaissances
-
Évaluation des savoir-faire
I. Auto-évaluation
3 = oui_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 2 = à peu près... _ _ _ _ _ _ _ _ _ 1 = pas encore!
Pensez‑vous maîtriser les savoirs et savoir‑faire suivants ?
‑Savoirs :
‑Savoir-faire :
II. Évaluation des connaissances
III.Évaluation des savoir-faire
|
♦ Ce que les programmes en disent...
|
-
Sciences éco, opt. base simple, 2e degré, 4 pér/sem (1994/0279/016)
-
Sciences éco, opt. base simple, 3e degré, 4 pér/sem (1994/0279/017)
-
Socio-économie, option, 1er degré, 2/4 pér/sem (1992/0279/081)
I. Sciences éco, opt. base simple, 2e degré, 4 pér/sem (1994/0279/016)
II. Sciences éco, opt. base simple, 3e degré, 4 pér/sem (1994/0279/017)
- Concurrence réelle : coût du capital (taux d'intérêt) p. 15
III.Socio-économie, option, 1er degré, 2/4 pér/sem (1992/0279/081)
♦ Sommaire, Introduction, Programmes et mots-clefs
-
Économie = ?
-
Contenu des étapes
-
Programmes de disciplines que vous êtes susceptibles de pouvoir enseigner
♦ ÉCONOMIE = Comment lire ce syllabus ?
-
Orientation générale
-
Les règles de lecture des étapes des premiers pas en économie
-
Quelques conseils complémentaires...
♦ Parabole de la veuve et des deux fils
-
Les personnages
-
Hypothèse 1 : partage de l'outil, chacun mange sa production
-
Hypothèse 1, variante
et la mère ? // chacun la moitié ? // et si le minimum vital est de 80 unités ? // et si le costaud participait plus ?
-
Hypothèse 2 : emploi de l'outil selon sa consommation
-
Les maths et l'économie
-
Le modèle : sa construction
-
Le modèle : son utilisation pour une production optimale
hypothèse 3 :repartition pour production optimale // production maximale // retenues optimisées
-
Et la concurrence ?
-
Présentation
-
Si la mère refuse...
-
Si la mère accepte...
-
Si le costaud exige plus, voire tout...
-
Le droit et l'économie
-
Les revenus de la propriété
3 heures à 10 unités, soit 30 unités // 3 heures à 40 unités, soit 120 unités // 3 heures à 16 unité, soit 48 unités // et si le petit bénéficiait d'un autre quota d'heures// quid le Cornélius et son outil inutilisé ?
-
Les notions abordées
♦ Une préparation type ?...Non ! (facture, note de débit, note de crédit)
♦ Et cette préparation est-elle type ? (indice et index)
♦ Algèbre financière : un sujet économique parmi d'autres...
-
Intérêts simples
-
exemple introductif
-
démonstration ou monstration
-
exemple chiffré et remarque
Quelle est la valeur acquise par 8500 €, placés sur un carnet d'épargne pendant 6 ans à 4,5 % (on retire les intérêts chaque année).. // Confusion intérêt (i) et taux d'intérêt (r)
-
Intérêts composés
-
définition
-
exemple introductif
-
démonstration ou monstration ?
-
Exemples chiffrés
Quelle est la valeur acquise par 8500 €, placés sur un carnet d'épargne pendant 6 ans à 4,5 % // Quelle est la valeur acquise par 8500 €, placés en bons de capitulation pendant 6 ans à 9 % (taux brut... donc 8,1 % net en début 93, devenant 7,7949 % net après le 01-01-94 et 7, 65 % depuis le 01-01-97... variation du précompte mobilier // et si le placement est fait pendant 5 ans et 7 mois ?
-
problèmes dérivés
Quelle somme faut-il placer à intérêts composés, pour obtenir Cn aprè n années ? // À quel taux faut-il placer à intérêts composés la somme Co pour obtenir Cn après n années ? // Pendant combien de temps dois-je placer au taux r, à intérêts composés, la somme Co pour obtenir le montant Cn ?
-
Annuités
-
définition
-
démonstration
-
Exemples chiffrés
-
problèmes dérivés
Quel est le montant à placer annuellement, pour obtenir après n versements au taux r, un capital A ? // Quelle est le nombre d'années pendant lesquelles je dois verser un montant pour obtenir A au taux r ?
-
Emprunts
-
démonstration
-
problèmes dérivés (plus fréquent)
Quel est le versement annuel, si j'emprunte V au taux r pendant n années ? // Quel remboursement annuel pour emprunter 1 million en 20 ans à 11 % ?
-
En résumé
-
Exercices
♦ À retenir
♦ Exercices et Travaux
I. Secteurs, Catégories et facteurs de production_ _ _ _ _ _ _ _ _ _ _ _ _ _ 79
♦ Évaluation des connaissances et des savoir-faire
-
Auto-évaluation
-
Évaluation des connaissances
-
Évaluation des savoir-faire
♦ Voir aussi...
♦ Ce que les programmes en disent...
-
Sciences éco, opt. base simple, 2e degré, 4 pér/sem (1994/0279/016)
-
Sciences éco, opt. base simple, 3e degré, 4 pér/sem (1994/0279/017)
-
Socio-économie, option, 1er degré, 2/4 pér/sem (1992/0279/081)
♦ Table des matières
[1] faut-il faire la distinction entre compétences disciplinaires et transversales ? L'une n'est-elle pas un prolongement de l'autre ?
[2] n'est-il pas préférable de pouvoir les distinguer plutôt que de pouvoir les définir ?
[3] Texte lacunaire avec trop de "trous"
[4] sans oublier le BE devenu obligatoire (en Belgique ! !) depuis 1996.
[5] Suggestion : commentaires sur cette numérotation, comment reconnaître les factures d'entrées (= achats) de celles de sotie (= vente)
[6] ces éléments sont à regrouper dans des rubriques : corps de facture, ...
[7] dans une préparation, il faut noter les "réponses"pour permettre une vérification de la part des chargéde cours et/ou maître de stage
[8] Un effort pour une mise en situation plus attractive
[9] orthographe SVP : "apprises"
[10] de quels documents s'agit-il ? ? Je suppose qu'il s'agit des feuilles élèves...
[11] précisez activités des e, méthode en cas de non succès, ...Ne serait-il pas tout aussi important de noter au TN "Quoi ? par qui ? pourquoi ?"qui suggère mieux une façon de retenir la définition, les éléments importants signalés et aussi une (meilleure) façon de noter cette définition ?
[12] Expression : "...dont tu te rappelles..."+ transition d'un point à l'autre à améliorer + structure à laisser plus apparente dans les étapes de cours
[13] Cette colonne activité de l'élève vide sous-entend-elle que les e dorment ? ?
N'est-il pas possible de noter les remarques méthodologiques en face de la matière vue ?
[14] on dira dans ce cas, un "concessionnaire"
[15] ton exemple ne risque-t-il pas d'être la même chose que ta définition (non notée ici) ?
[16] très bien, ceci montre la condition : SI...
[17] la question me semble trop floue pour engendrer cette réponse (erreur de genre) de la part des e.
[18] es-tu sûr que ce ne soit pas sur le total à payer ? ?
[19] plus tôt que....À PRÉCISER
[20] plutôt que de demander "QUAND ?", il pourrait être intéressant de demander "À QUELLE CONDITION ?"(escompte conditionnel)
[21] Pour le problème du doublement à intérêts composés, on emploie parfois une approximation dite "règle des 70" : à 4 % il faut 17,6 ans ; 8 % il faut 9 ans…
Retour à la page d'accueil de CUY = See you why ?

Compteur gratuit

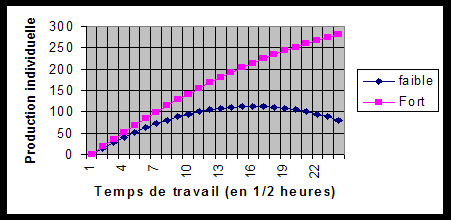



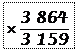

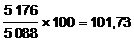 .
.